L’errore standard della media, o semplicemente errore standard, indica quanto sia diversa la media della popolazione da una media campione. Ti dice quanto la media del campione varierebbe se dovessi ripetere uno studio usando nuovi campioni all’interno di una singola popolazione.
L’errore standard della media (SE o SEM) è il tipo di errore standard più comunemente riportato. Ma puoi anche trovare l’errore standard per altre statistiche, come mediane o proporzioni. L’errore standard è una misura comune di errore di campionamento – la differenza tra un parametro di popolazione e una statistica del campione.
Perché l’errore standard è importante
Nelle statistiche, i dati provenienti dai campioni vengono utilizzati per comprendere popolazioni più grandi. L’errore standard è importante perché ti aiuta a stimare quanto bene i tuoi dati di esempio rappresentano l’intera popolazione.
Con il campionamento probabilistico, in cui gli elementi di un campione sono selezionati in modo casuale, è possibile raccogliere dati che potrebbero essere rappresentativi della popolazione. Tuttavia, anche con campioni di probabilità, rimarrà qualche errore di campionamento. Questo perché un campione non corrisponderà mai perfettamente alla popolazione da cui proviene in termini di misure come mezzi e deviazioni standard.
Calcolando l’errore standard, puoi stimare quanto il tuo campione sia rappresentativo della tua popolazione e trarre conclusioni valide.
Un errore standard elevato mostra che i mezzi del campione sono ampiamente diffusi attorno alla media della popolazione: il campione potrebbe non rappresentare da vicino la popolazione. Un errore standard basso mostra che i mezzi del campione sono strettamente distribuiti attorno alla media della popolazione: il campione è rappresentativo della popolazione.
È possibile ridurre l’errore standard aumentando la dimensione del campione. L’utilizzo di un campione ampio e casuale è il modo migliore per ridurre al minimo il bias di campionamento.
Errore standard vs deviazione standard
Errore standard e deviazione standard sono entrambe misure di variabilità:
- La deviazione standard descrive la variabilità all’interno di un singolo campione.
- L’errore standard stima la variabilità tra più campioni di una popolazione.


La deviazione standard è una statistica descrittiva, che può essere calcolato da dati di esempio. Al contrario, l’errore standard è una statistica inferenziale che può essere stimata solo (a meno che non sia noto il parametro della popolazione reale).
La deviazione standard dei punteggi matematici è 180. Questo numero riflette in media quanto ciascun punteggio differisce dal punteggio medio del campione di 550.
L’errore standard dei punteggi matematici, d’altra parte, ti dice quanto il punteggio medio del campione di 550 differisce da altri punteggi medi del campione, in campioni di uguali dimensioni, nella popolazione di tutti i test takers nella regione.
errore Standard formula
L’errore standard della media è calcolata utilizzando la deviazione standard e la dimensione del campione.
Dalla formula, vedrai che la dimensione del campione è inversamente proporzionale all’errore standard. Ciò significa che più grande è il campione, minore è l’errore standard, perché la statistica del campione sarà più vicina all’avvicinamento al parametro della popolazione.
Vengono utilizzate formule diverse a seconda che la deviazione standard della popolazione sia nota. Queste formule funzionano per campioni con più di 20 elementi (n > 20).
Quando i parametri della popolazione sono noti
Quando la deviazione standard della popolazione è nota, è possibile utilizzarla nella formula seguente per calcolare con precisione l’errore standard.
| Formula | Spiegazione |
|---|---|
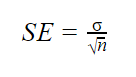 |
|
Quando i parametri di popolazione sono sconosciuti
Quando la deviazione standard della popolazione è sconosciuta, è possibile utilizzare la formula qui di seguito solo stima errore standard. Questa formula prende la deviazione standard del campione come stima puntuale per la deviazione standard della popolazione.
| Formula | Spiegazione |
|---|---|
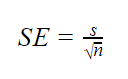 |
|
Innanzitutto, trova la radice quadrata della dimensione del campione (n).
| Formula | Calcolo |
|---|---|
| √n | n = 200
√n = √200 = 14.1 |
Quindi, dividere la deviazione standard del campione per il numero trovato nel primo passaggio.
| Formula | Calcolo |
|---|---|
| SE = s ś √n | s = 180
√n = 14.1 s ÷ √n = 180 ÷ 14.1 = 12.8 |
L’errore standard della matematica punteggi SAT è 12.8.
Come si deve segnalare l’errore standard?
È possibile segnalare l’errore standard accanto alla media o in un intervallo di confidenza per comunicare l’incertezza attorno alla media.
Il modo migliore per segnalare l’errore standard è in un intervallo di confidenza perché i lettori non dovranno fare alcuna matematica aggiuntiva per ottenere un intervallo significativo.
Un intervallo di confidenza è un intervallo di valori in cui si prevede che un parametro di popolazione sconosciuto si trovi la maggior parte del tempo, se si dovesse ripetere lo studio con nuovi campioni casuali.
Con un livello di confidenza del 95%, il 95% di tutte le medie del campione dovrebbe trovarsi entro un intervallo di confidenza di ± 1,96 errori standard della media del campione.
In base al campionamento casuale, si stima che anche il parametro della popolazione reale si trovi all’interno di questo intervallo con una confidenza del 95%.
Per una caratteristica normalmente distribuita, come i punteggi SAT, il 95% di tutti i mezzi del campione rientra in circa 4 errori standard della media del campione.
| intervallo di Confidenza formula | |
|---|---|
|
CI = x ± (1.96 × SE) x = media del campione = 550 |
|
| limite Inferiore | limite Superiore |
|
x − (1.96 × SE) 550 − (1.96 × 12.8) = 525 |
x + (1.96 × SE) 550 + (1.96 × 12.8) = 575 |
Con il campionamento casuale, un IC al 95% ti dice che c’è una probabilità 0.95 che il punteggio SAT math medio della popolazione sia compreso tra 525 e 575.
Altri errori standard
A parte l’errore standard della media (e altre statistiche), ci sono altri due errori standard che potresti incontrare: l’errore standard della stima e l’errore standard di misurazione.
L’errore standard della stima è correlato all’analisi di regressione. Ciò riflette la variabilità attorno alla linea di regressione stimata e l’accuratezza del modello di regressione. Utilizzando l’errore standard della stima, è possibile costruire un intervallo di confidenza per il coefficiente di regressione vero.
L’errore standard di misurazione riguarda l’affidabilità di una misura. Indica quanto è variabile l’errore di misurazione di un test ed è spesso riportato nei test standardizzati. L’errore standard di misura può essere utilizzato per creare un intervallo di confidenza per il vero punteggio di un elemento o di un individuo.
Domande frequenti sull’errore standard
L’errore standard della media, o semplicemente errore standard, indica quanto è probabile che la media della popolazione sia diversa da una media campione. Ti dice quanto la media del campione varierebbe se dovessi ripetere uno studio usando nuovi campioni all’interno di una singola popolazione.
Errore standard e deviazione standard sono entrambe misure di variabilità. La deviazione standard riflette la variabilità all’interno di un campione, mentre l’errore standard stima la variabilità tra i campioni di una popolazione.
Utilizzando le statistiche descrittive e inferenziali, è possibile effettuare due tipi di stime sulla popolazione: stime puntuali e stime degli intervalli.
- Una stima puntuale è una stima del valore singolo di un parametro. Ad esempio, una media campione è una stima puntuale di una media di popolazione.
- Una stima dell’intervallo fornisce un intervallo di valori in cui si prevede che il parametro si trovi. Un intervallo di confidenza è il tipo più comune di stima dell’intervallo.
Entrambi i tipi di stime sono importanti per raccogliere un’idea chiara di dove un parametro è probabile che si trovi.
