de standaardfout van het gemiddelde, of gewoon standaardfout, geeft aan hoe verschillend het populatiegemiddelde waarschijnlijk zal zijn van een steekproefgemiddelde. Het vertelt je hoeveel het steekproefgemiddelde zou variëren als je een studie zou herhalen met behulp van nieuwe steekproeven binnen een enkele populatie.
de standaardfout van het gemiddelde (SE of SEM) is het meest gerapporteerde type standaardfout. Maar je kunt ook de standaardfout vinden voor andere statistieken, zoals medianen of proporties. De standaardfout is een gemeenschappelijke maat voor de steekproeffout—het verschil tussen een populatieparameter en een steekproefstatistiek.
waarom standaardfouten belangrijk zijn
in statistieken worden gegevens uit steekproeven gebruikt om grotere populaties te begrijpen. Standaardfout is belangrijk omdat het U helpt in te schatten hoe goed uw steekproefgegevens de hele populatie vertegenwoordigen.
met kanssteekproef, waarbij elementen van een steekproef willekeurig worden geselecteerd, kunt u gegevens verzamelen die waarschijnlijk representatief zijn voor de populatie. Echter, zelfs met kanssteekproeven, zal sommige steekproeffout blijven. Dat komt omdat een steekproef nooit perfect zal overeenkomen met de populatie waar het vandaan komt in termen van maatregelen zoals middelen en standaardafwijkingen.
door de standaardfout te berekenen, kunt u inschatten hoe representatief uw steekproef is voor uw populatie en geldige conclusies trekken.
een fout met hoge standaard laat zien dat de gemiddelden van de steekproef wijd verspreid zijn over het populatiegemiddelde—uw steekproef vertegenwoordigt mogelijk niet nauw uw populatie. Een lage standaardfout toont aan dat de steekproefmiddelen nauw zijn verdeeld over het bevolkingsgemiddelde—uw steekproef is representatief voor uw populatie.
u kunt de standaardfout verkleinen door de steekproefgrootte te vergroten. Met behulp van een grote, willekeurige steekproef is de beste manier om bemonstering bias te minimaliseren.
standaardfout vs standaarddeviatie
standaardfout en standaarddeviatie zijn beide variabiliteitsmaten:
- de standaardafwijking beschrijft de variabiliteit binnen één monster.
- de standaardfout schat de variabiliteit tussen meerdere steekproeven van een populatie.


de standaardafwijking is een beschrijvende statistiek die kan worden berekend aan de hand van steekproefgegevens. De standaardfout is daarentegen een inferentiële statistiek die alleen kan worden geschat (tenzij de werkelijke populatie parameter bekend is).
de standaardafwijking van de wiskundescores is 180. Dit aantal weerspiegelt gemiddeld hoeveel elke score verschilt van de steekproef gemiddelde score van 550.
de standaardfout van de wiskundescores daarentegen geeft aan in hoeverre de gemiddelde score van de steekproef van 550 verschilt van de gemiddelde score van de andere steekproefscores, in monsters van gelijke grootte, in de populatie van alle testnemers in de regio.
Standaardfoutformule
de standaardfout van het gemiddelde wordt berekend aan de hand van de standaardafwijking en de steekproefgrootte.
uit de formule zult u zien dat de steekproefgrootte omgekeerd evenredig is met de standaardfout. Dit betekent dat hoe groter de steekproef, hoe kleiner de standaardfout, omdat de steekproefstatistiek dichter bij het naderen van de populatieparameter zal zijn.
verschillende formules worden gebruikt naargelang de standaardafwijking van de populatie bekend is. Deze formules werken voor monsters met meer dan 20 elementen (n > 20).
wanneer populatieparameters bekend zijn
wanneer de standaardafwijking van de populatie bekend is, kunt u deze in de onderstaande formule gebruiken om de standaardfout nauwkeurig te berekenen.
| formule | uitleg |
|---|---|
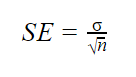 |
|
als populatie parameters onbekend zijn
als de populatie standaarddeviatie onbekend is, kunt u de onderstaande formule gebruiken om alleen de standaardfout te schatten. Deze formule neemt de standaardafwijking van de steekproef als puntschatting voor de standaardafwijking van de populatie.
| formule | uitleg |
|---|---|
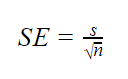 |
|
zoek eerst de vierkantswortel van uw steekproefgrootte (n).
| formule | berekening |
|---|---|
| √n | n = 200
√n = √200 = 14.1 |
verdeel vervolgens de standaarddeviatie van het monster door het nummer dat u in stap één hebt gevonden.
| formule | berekening |
|---|---|
| SE = s ÷ √n | s = 180
√n = 14,1 s ÷ √n = 180 ÷ 14.1 = 12.8 |
de standaard fout van wiskunde SAT scores is 12,8.
Hoe moet u de standaardfout rapporteren?
u kunt de standaardfout naast het gemiddelde of in een betrouwbaarheidsinterval rapporteren om de onzekerheid rond het gemiddelde te communiceren.
de beste manier om de standaardfout te rapporteren is in een betrouwbaarheidsinterval, omdat lezers geen extra wiskunde hoeven te doen om met een zinvol interval te komen.
een betrouwbaarheidsinterval is een bereik van waarden waarbij een onbekende populatieparameter naar verwachting het grootste deel van de tijd zal liggen als u uw onderzoek met nieuwe aselecte steekproeven zou herhalen.
bij een betrouwbaarheidsniveau van 95% zal naar verwachting 95% van alle gemiddelden in de steekproef liggen binnen een betrouwbaarheidsinterval van ± 1,96 standaardfouten van het gemiddelde in de steekproef.
op basis van aselecte steekproeven wordt ook de werkelijke populatieparameter geschat binnen dit bereik te liggen met een betrouwbaarheid van 95%.
voor een normaal gedistribueerde eigenschap, zoals SAT-scores, valt 95% van alle steekproefgemiddelden binnen ongeveer 4 standaardfouten van het steekproefgemiddelde.
| formule voor betrouwbaarheidsinterval | |
|---|---|
|
BI = x ± (1,96 × SE) x = monstergemiddelde = 550 |
|
| ondergrens | bovengrens |
|
x- (1.96 × SE) 550 − (1.96 × 12.8) = 525 |
x + (1,96 × SE) 550 + (1.96 × 12.8) = 575 |
met willekeurige steekproeven, vertelt een 95% BI u dat er een 0.95 waarschijnlijkheid is dat de bevolking gemiddelde math SAT score tussen 525 en 575 is.
andere standaardfouten
naast de standaardfout van het gemiddelde (en andere statistieken), zijn er nog twee andere standaardfouten die u kunt tegenkomen: de standaardfout van de schatting en de standaardfout van de meting.
de standaardfout van de schatting is gerelateerd aan de regressieanalyse. Dit weerspiegelt de variabiliteit rond de geschatte regressielijn en de nauwkeurigheid van het regressiemodel. Met behulp van de standaardfout van de schatting kunt u een betrouwbaarheidsinterval voor de werkelijke regressiecoëfficiënt construeren.
de standaardfout van de meting gaat over de betrouwbaarheid van een meting. Het geeft aan hoe variabel de meetfout van een test is, en het wordt vaak gerapporteerd in gestandaardiseerde tests. De standaardfout van de meting kan worden gebruikt om een betrouwbaarheidsinterval te creëren voor de werkelijke score van een element of een individu.
Veelgestelde vragen over standaardfout
de standaardfout van het gemiddelde, of gewoon de standaardfout, geeft aan hoe verschillend het populatiegemiddelde waarschijnlijk is van een steekproefgemiddelde. Het vertelt je hoeveel het steekproefgemiddelde zou variëren als je een studie zou herhalen met behulp van nieuwe steekproeven binnen een enkele populatie.
standaardfout en standaarddeviatie zijn beide variabiliteitsmaten. De standaardafwijking weerspiegelt de variabiliteit binnen een steekproef, terwijl de standaardafwijking de variabiliteit tussen steekproeven van een populatie schat.
met behulp van beschrijvende en inferentiële statistieken kunt u twee soorten schattingen maken over de populatie: puntschattingen en intervalschattingen.
- een puntschatting is een enkele waardeschatting van een parameter. Bijvoorbeeld, een steekproefgemiddelde is een puntschatting van een populatiegemiddelde.
- een intervalschatting geeft u een bereik van waarden waar de parameter naar verwachting zal liggen. Een betrouwbaarheidsinterval is de meest voorkomende soort intervalschatting.
beide soorten schattingen zijn belangrijk om een duidelijk beeld te krijgen van waar een parameter waarschijnlijk zal liggen.
