hoe p-waarde berekenen in Excel?

Inhoud

1. 1. Wat Is De P-Waarde?
   2. Waarom Hebben We De P-Waarde Nodig?
   3. Waar Gebruiken We De P-Waarde In Het Echte Leven?
      • Marketing
      • waarschijnlijkheid
   4. hoe de P-waarde in Excel berekenen?
   5. laatste woorden

Wat is de P-waarde?

P-waarde is een statistische term die u helpt om, als de hypothese die u gebruikt waar is, de waarschijnlijkheid van de steekproefvariatie te bepalen. Het vertelt ons gewoon wat de kansen zijn om deze resultaten te krijgen als onze nulhypothese waar is.

• een nulhypothese is een hypothese die beweert dat de resultaten die we krijgen veroorzaakt worden door puur geluk.
• een alternatieve hypothese beweert dat de resultaten die we krijgen geen geluk zijn, maar dat er externe elementen zijn die onze resultaten beïnvloeden.

het is een zeer belangrijke en veelgebruikte statistische term en kan gemakkelijk worden berekend in data-analyse programma ‘ s zoals Microsoft Excel. In dit artikel leert u hoe we het gebruiken, waar we het gebruiken en hoe we het op verschillende manieren in Excel kunnen berekenen.

laten we beginnen!

Waarom Hebben We De P-Waarde Nodig?

bij onderzoek met grote populaties moet u de statistieken voor elk individu berekenen. Maar zelfs in zo ‘ n geval Weet je niet zeker of er iets gebeurd is vanwege toeval of gewoon geluk, omdat het onmogelijk is om alles waar te nemen. Dit is waar statistieken van belang zijn.

statistische berekeningen kunnen u geen absolute waarheid geven, maar ze zullen u helpen een goed beeld te krijgen van uw onderzoeken.

P-waarde stelt ons in staat om de hypothese op ons onderwerp te testen. We kunnen de wiskundige resultaten vergelijken met deze hypothesen en ons pad heroverwegen zonder veel tijd aan onderzoek te besteden.

Waar Gebruiken We De P-Waarde In Het Echte Leven?

we gebruiken de waarschijnlijkheidswaarde wanneer we een hypothese proberen te testen. Het kan over onderzoek gaan of een simpele weddenschap die we met onze vriend hebben gemaakt.

het is gemakkelijker te begrijpen met voorbeelden.

Marketing:

stel dat u werkzaam bent op het gebied van marketing en dat uw recente project betrekking heeft op reclame voor granen.

u hebt een video voor sociale media geproduceerd en u hebt de informatie voor eerder gebruikers overgeslagen of bekeken voor een lange tijd.

als voorbeeld: de normale kijktijd van de video is 20 seconden. Het gemiddelde is 20 seconden. En je nam de beslissing om de video te bewerken met een stuk vreugdevolle Muziek.

hoe herkent u nu of het werkte? Op dit punt gebruiken we significantiestatistieken.

produceer eerst een nulhypothese:

een nulhypothese beweert dat er geen correlatie is tussen wat u investeert en de resultaten die u krijgt. Het heeft geen invloed op de resultaten.

in dit voorbeeld zal de nulhypothese als volgt zijn: “er is geen verband tussen de wijzigingen die u toepast op de kijktijd.”

toen, de alternatieve hypothese:

de alternatieve hypothese suggereert dat het veranderen van de muziek werkte en nu mensen kijken naar de commercial voor meer dan 20 seconden. Wiskundig gezien zegt de alternatieve hypothese:

” het gemiddelde is nu meer dan 20 seconden.”

Bereken het significantieniveau:

nu moeten we een grensdrempel Instellen om te berekenen of we succesvol zijn of niet. Dit heet een betekenis niveau wordt bovendien aangeduid als de alpha-waarde. Het kan elk percentage zijn dat je wilt, het is absoluut aan jou.

maar in dit voorbeeld zal het 0,05 zijn.

om met zekerheid te kunnen berekenen, moeten we altijd alle gegevens van de kijktijd hebben. Maar in termen van tijd en bronnen, moet je een monster nemen van de bevolking:

1. u nam een steekproef van 100 personen.
2. deze 100 mensen hebben 25 seconden kijktijd voor de reclame.
3. het betekent dat het steekproefgemiddelde 25 is.

dit is een zeer eenvoudige versie van de berekening. Maar de standaardafwijking van de steekproef wordt meestal op deze schaal berekend als je de standaardafwijking van de gehele populatie niet kent.

u kunt de waarden die u voor de steekproef hebt berekend, gebruiken omdat ze dicht bij de populatiewaarden liggen. Het steekproefgemiddelde ligt dicht bij het populatiegemiddelde.

Bereken de P-waarde:

de p-waarde laat ons zien of we de nulhypothese al dan niet kunnen afwijzen. De kans dat het steekproefgemiddelde groter is dan of gelijk is aan 25 minuten gegeven de nulhypothese is waar.

er kunnen zich twee situaties voordoen.

1. als de p-waarde kleiner is dan de Alfa kunt u de nulhypothese afwijzen. Je hebt statistisch bewijs dat de alternatieve hypothese waar is.
2. maar als de p-waarde groter of gelijk is aan de Alfa kunt u de nulhypothese niet afwijzen. Het betekent niet dat de nulhypothese zeker waar is, maar het kan ook niet worden vermeden.

kans

laten we aan een ander voorbeeld werken.

je vriend en je gooide munt in de lucht: als het munt is verlies je 5 dollar en als het kop komt krijg je 5 dollar.

• uw vriend gooit de munt één keer: het komt als munt. Het is goed, er is een 50% kans dat het als munt komt. Nu ga je ervan uit dat de kans 0,5 is omdat je gelooft dat het een eerlijke munt is. Dit is je nulhypothese.

• tweede: het is staarten. Je verloor nog eens 5 dollar, maar het is goed, want er is nog steeds een goede kans op twee staarten op een Rij. De p-waarde is 0,25 en het is nog steeds een redelijke verhouding.
• derde: het is weer staarten. De kans op staarten drie keer achter elkaar is 0,12. Het is niet laag dus er is niet genoeg bewijs dat de nulhypothese niet correct is. Maar je begint te denken dat je alternatieve hypothese juist zou kunnen zijn.
• vierde: het draait weer als staarten je zult zien hoe de kansen echt laag worden. Het kan een wonderbaarlijk toeval zijn, maar er is nog steeds een 0,6 kans en er is nog steeds niet genoeg bewijs om de alternatieve hypothese te ondersteunen dat de munt lastig is. En je wacht op de vijfde Salto.
• vijfde: het is staarten. De kans dat een munt vijf keer achter elkaar munt wordt is 0,3 wat erg laag is. Dit is het punt waarop je de nulhypothese kunt afwijzen want er is niet genoeg bewijs om het meer te ondersteunen.

je vraagt je vriend om de munt te zien en als je hem vasthoudt besef je dat hij twee staarten heeft en dat het een lastige munt is.

wat heeft ervoor gezorgd dat we het vertrouwen in onze nulhypothese verloren?

in een eerlijk spel van het omgooien van munten is de kans op een kop of een munt 50%. Dit is een situatie waarin we geloven dat de munt eerlijk is, maar als de p-waarde daalt ons vertrouwen in die hypothese verzwakt ook.

er is weinig kans op willekeurige staarten wanneer de p-waarde onder 0,05 daalt. Dus als je deze statistische term toepast op zaken als kankeronderzoek of effecten van klimaatverandering, wordt het belangrijker.

Opmerking: Er is geen specifieke reden waarom we 0,05 p-waarde gebruiken voor standaardberekening. De maker van de formule besloot dat het een goed getal was voor het berekenen en de standaardberekeningen blijven erbij. 0,05 betekent 5% in 100 individuele populaties die in de normale curve valt. Dit is een van de redenen dat het vaak wordt gebruikt. Als je het zelf wilt veranderen tijdens het berekenen, kan dat.

hoe de P-waarde in Excel berekenen?

er is meer dan één manier om de p-waarde in Microsoft Excel te berekenen. U kunt formules typen of u kunt Analysis ToolPak gebruiken. Dit artikel bevat hoe het op beide manieren te doen.

gebruik van klassieke Excel-formules:

laten we beginnen met de klassieke Excel-formule. Er zijn twee manieren om deze TDIST formule en T-test formule te doen.

1.1) TDIST-formule

allereerst hebt u een gegevensset nodig om een p-waarde te berekenen.

• stel dat u een leraar bent en u wilt vergelijken wat uw leerlingen scoorden in uw laatste examen en wat u verwachtte dat hun score zou zijn gebaseerd op hun vorige examens.
• u heeft de resultaten 25, 46, 34, 27, 35, 43, 40, 44, 21 en 39 voor je laatste examen.
• voor de berekening heb je een andere staart nodig, dit is de score die je verwachtte op basis van eerdere tests: 23, 44, 32, 20, 46, 37, 35, 42, 33, en 35

nu, om de p-waarde-formule op Excel te gebruiken, moet u vooraf een paar dingen berekenen:

Pearson-coëfficiënt (r): Het is een statistische term die de lineaire correlatie tussen twee gegevens meet. Je hoeft het wiskundige aspect ervan niet te kennen om de p-waarde te berekenen. U zult de eenvoudige formule ervoor zien in de volgende alinea ‘ s.

populatie (n): n is het totale aantal personen in uw gegevensverzameling.

T statistieken: het is de verhouding tussen de afwijking van de geschatte waarde van de gegevens van de veronderstelde waarde en de standaardfout.

vrijheidsgraad: het aantal individuen in de gegevensverzameling min twee.

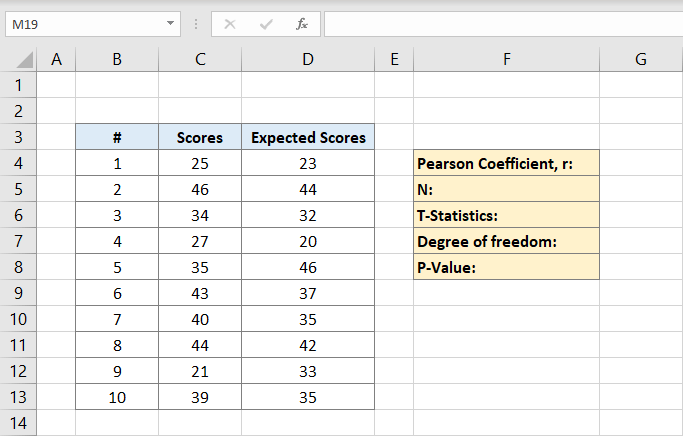
nu, de Pearson coëfficiënt zal worden geschreven op F4 in dit voorbeeld. Nadat u erop hebt geklikt, typt u de formule:

C-kolommen zijn voor de scores en D-kolommen zijn voor de verwachte scores. De Pearson coëfficiënt is 0,691473 in dit voorbeeld.

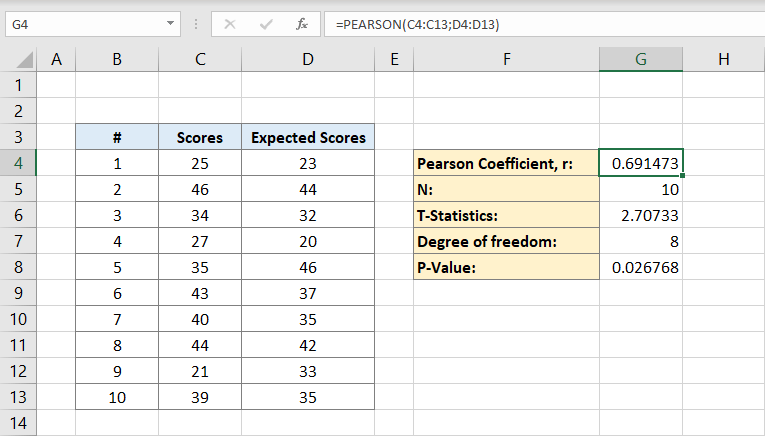
vervolgens typt u het aantal personen in de dataset. Als je zeker weet hoeveel mensen je hebt kunt u het handmatig typen, maar als je niet kunt u de formule gebruiken:

waarom bevat de formule alleen een kolom C?

het is omdat we alleen de individuen in één gegevensverzameling nodig hebben om te berekenen, daarom is één kolom voldoende. De cel G5 bevat nu het nummer 10 erin. Dit is onze bevolking.

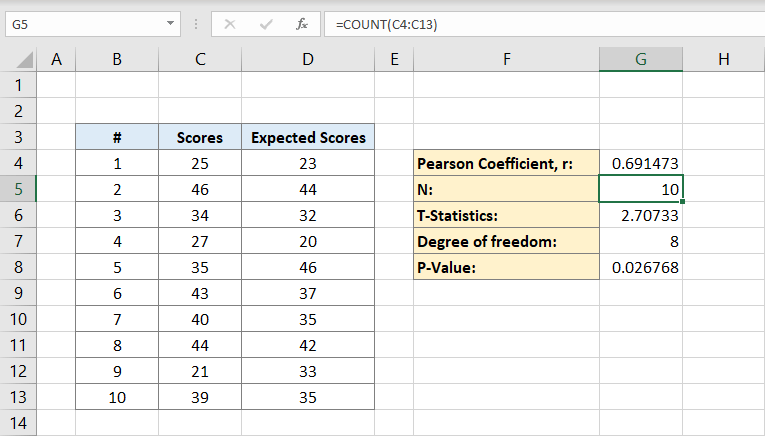
nu je zowel de Pearson-coëfficiënt als de populatie hebt, kun je T-statistieken berekenen. De wiskundige formule voor t-statistieken is de Pearson-coëfficiënt (r) maalteken vierkantswortel van de populatie (n) min 2 gedeeld door de vierkantswortel van 1 min Pearson-coëfficiënt kwadraat:

de cel G6 zal het resultaat 2,70733 bevatten. Dit is onze T-statistiek.

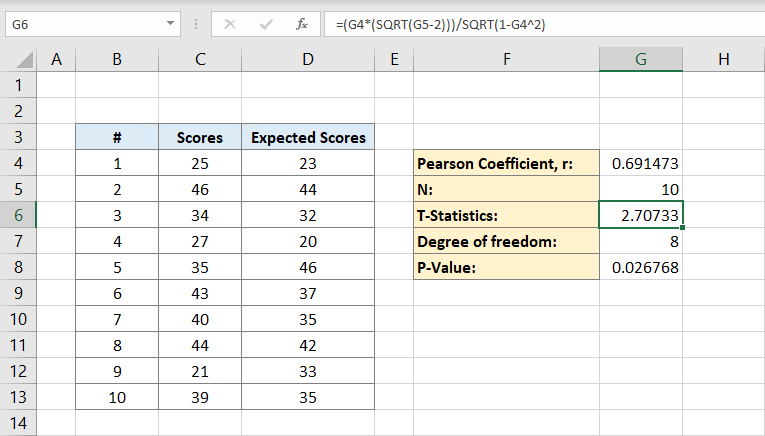
daarna bereken je de mate van vrijheid. U typt:

naar de cel G7. Dit is de mate van vrijheid. Het zal om acht uur zijn.

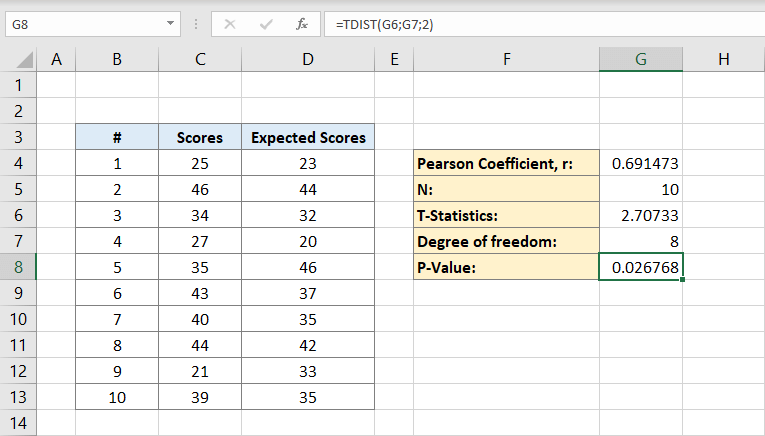
nu heb je alles wat je nodig hebt om de P-waarde te berekenen. De cel G8 zal er de formule voor bevatten. Dat wil zeggen:

of

het resultaat zal 0,026768 zijn. Dit is de p-waarde voor de dataset.

1.2. T-Testformule

de tweede manier om de p-waarde met Excel-formules te bepalen, is met behulp van de T-testformule. Het is een beetje vergelijkbaar met het vorige voorbeeld, maar korter.

• stel dat de dataset hetzelfde is, je hebt de resultaten 25, 46, 34, 27, 35,43, 40, 44, 21, 39 voor je laatste examen.
• verwachte resultaten zijn 23, 44, 32, 20, 46, 37, 35, 42, 33, 35.
• u gaat een derde kolom toevoegen voor het verschil tussen wat werd verwacht en de werkelijke score. In de kolom verschil 2, 2, 2, 7, 11, 6, 5, 2, 12, 4 wordt geschreven van E4 naar E13.

typ nu t-Test in cel E8. Je gaat de T-test formule schrijven naar de lege cel ernaast. Dat wil zeggen:

en deze formule geeft u de p-waarde direct.

Bepaal de P-waarde met Excel Tool Pak

Took Pak is een pakket waarmee u verschillende statistische metingen automatisch kunt berekenen, dus het is gemakkelijk en erg handig. Het is ook eenvoudig te installeren.

Stap 1: Ga naar Instellingen. Er is een “Add-ins” knop aan de onderkant van de linkerhoek, klik erop. Een nieuw venster verschijnt, vind de “Analysis Tool Pak” optie, klik erop, en klik vervolgens op de knop go aan de onderkant van het venster.

Stap 2: Activeer de invoegtoepassing door op het vinkje ernaast en na de OK knop in de rechterkolom te klikken.

Stap 3: als het u gelukt is om het correct te activeren, verschijnt er een knop “Data analysis” in het bovenste menu van uw werkblad aan de rechterkant.

Stap 4: Klik op de knop” Data analysis “en kies de optie” t-Test: Paired Two Sample for Means”. Klik daarna op OK. Er verschijnt een nieuw venster.

Stap 5: Het vraagt de invoer in de eerste rij van het venster. Type C4: C13 naar het vak” variabel 1 bereik”. U typt D4: D13 in het vak” variable 2 range”. Laat de alpha box met zijn standaard waarde.

Stap 6: in de tweede rij van het venster kunt u selecteren waar u uw resultaten wilt controleren. Het kan een nieuw werkblad of lege cellen zijn. Als u het resultaat op een cel wilt, moet u de kolom en de rij vergrendelen. Klik daarna op de OK knop.

Tip: Gebruik het dollarteken voor de letter en het nummer om de kolom en rij te vergrendelen. Als u bijvoorbeeld A2-cel wilt vergrendelen, typt u $A$2.

Stap 7: de Excel berekent het gemiddelde, variantie, waarnemingen, Pearson correlatie, veronderstelde gemiddelde verschil, t statistieken, p-waarde, en meer.

laatste woorden

P-waarde is gemakkelijk te berekenen en aan te passen in veel verschillende situaties. Het helpt u om de informatie die u nodig hebt zonder de uitgaven veel tijd of moeite op. Het is nog gemakkelijker om te berekenen wanneer u statistische analyse programma ‘ s zoals Microsoft Excel die worden geleverd met de juiste tools en formules te gebruiken. Laten we eens kijken Someka templates collectie en download statistische sjablonen om uw werk gemakkelijker te maken!

gerelateerde metingen:

• hoe het betrouwbaarheidsinterval in Excel berekenen?
• Kan Excel Gegevens Analyseren?