i statistikk er det fire datamålevekter: nominell, ordinal, intervall og forhold. Dette er bare måter å sub-kategorisere ulike typer data (her er en oversikt over statistiske datatyper) . Dette emnet diskuteres vanligvis i sammenheng med akademisk undervisning og sjeldnere i den «virkelige verden.»Hvis du pusser opp på dette konseptet for en statistikktest, takk en psykologforsker Ved Navn Stanley Stevens for å komme opp med disse vilkårene.
disse fire datamåleskalaene (nominell, ordinal, intervall og forhold) forstås best med eksempel, som du vil se nedenfor.
Nominell
la oss starte med det enkleste å forstå. Nominelle skalaer brukes til merking av variabler, uten kvantitativ verdi. «Nominelle» skalaer kan ganske enkelt kalles » etiketter.»Her er noen eksempler, nedenfor. Legg merke til at alle disse skalaene er gjensidig utelukkende (ingen overlapping) og ingen av dem har noen numerisk betydning. En god måte å huske alt dette på er at «nominell» høres mye ut som » navn «og nominelle skalaer er slags som» navn » eller etiketter.
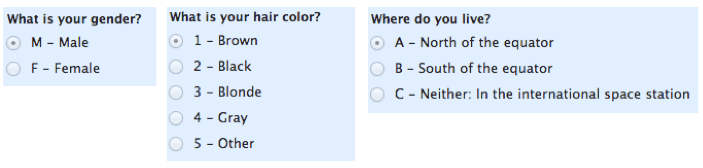
Merk: en undertype av nominelle skalaer med kun to kategorier (f.eks. mann/kvinne) kalles «dikotom.»Hvis du er student, kan du bruke det til å imponere læreren din .
Bonus Notat # 2: Andre undertyper av nominelle data er » nominell med ordre «(som» kald, varm, varm, veldig varm») og nominell uten ordre (som»mann/kvinne»).
Ordinær
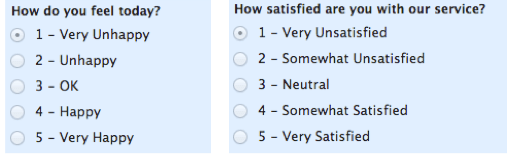
med ordinære skalaer er rekkefølgen av verdiene det som er viktig og signifikant, men forskjellene mellom hver enkelt er egentlig ikke kjent. Ta en titt på eksemplet nedenfor. I hvert tilfelle vet vi at en # 4 er bedre enn en #3 eller #2, men vi vet ikke–og kan ikke kvantifisere–hvor mye bedre det er. For eksempel er forskjellen MELLOM» OK » OG «Ulykkelig» det samme som forskjellen mellom «Veldig Glad» og » Glad?»Vi kan ikke si.
Ordinære skalaer er vanligvis tiltak av ikke-numeriske begreper som tilfredshet, lykke, ubehag, etc.
» Ordinal «er lett å huske fordi det høres ut som» orden», og det er nøkkelen til å huske med»ordensskalaer» –det er rekkefølgen som betyr noe, men det er alt du virkelig får fra disse.
Avansert merk: den beste måten å bestemme sentral tendens på et sett med ordensdata er å bruke modusen eller medianen; en purist vil fortelle deg at gjennomsnittet ikke kan defineres fra et ordenssett.
Intervall
Intervallskalaer er numeriske skalaer der vi kjenner både rekkefølgen og de eksakte forskjellene mellom verdiene. Det klassiske eksemplet På en intervallskala Er Celsius temperatur fordi forskjellen mellom hver verdi er den samme. For eksempel er forskjellen mellom 60 og 50 grader en målbar 10 grader, som er forskjellen mellom 80 og 70 grader.
Intervallskalaer er fine fordi riket av statistisk analyse på disse datasettene åpnes. For eksempel kan sentral tendens måles ved modus, median eller middel; standardavvik kan også beregnes.
som de andre, kan du huske de viktigste punktene i en «intervallskala» ganske enkelt. «Intervall» i seg selv betyr «mellomrom i mellom», noe som er viktig å huske-intervallskalaer forteller oss ikke bare om orden, men også om verdien mellom hvert element.
her er problemet med intervallskalaer: de har ikke en » sann null.»For eksempel er det ikke noe som «ingen temperatur», i hvert fall ikke med celsius. I tilfelle av intervallskalaer betyr null ikke fravær av verdi, men er faktisk et annet tall som brukes på skalaen, som 0 grader celsius. Negative tall har også betydning. Uten en sann null er det umulig å beregne forholdstall. Med intervalldata kan vi legge til og trekke fra, men kan ikke multiplisere eller dele.
Forvirret? Ok, vurder dette: 10 grader C + 10 grader C = 20 grader C. Ikke noe problem der. 20 grader C er ikke dobbelt så varmt som 10 grader C, men fordi det ikke er noe slikt som «ingen temperatur» når Det gjelder Celsius-skalaen. Når det konverteres Til Fahrenheit, er DET klart: 10C=50F OG 20C=68F, som tydeligvis ikke er dobbelt så varmt. Jeg håper det gir mening. Bunnlinjen, intervallskalaer er gode, men vi kan ikke beregne forhold, noe som bringer oss til vår siste måleskala…

Forhold
Forholdsskalaer er det ultimate nirvana når det gjelder datamåleskalaer fordi de forteller oss om rekkefølgen, de forteller oss den nøyaktige verdien mellom enheter, OG de har også et absolutt null–som gjør det mulig å bruke et bredt spekter av både beskrivende og inferensiell statistikk. Med fare for å gjenta meg selv, gjelder alt over om intervalldata for forholdsskalaer, pluss forholdsskalaer har en klar definisjon av null. Gode eksempler på forholdsvariabler inkluderer høyde, vekt og varighet.
Ratio skalaer gir et vell av muligheter når det gjelder statistisk analyse. Disse variablene kan menings lagt, subtraheres, multiplisert, delt (forholdstall). Sentral tendens kan måles ved modus, median, eller mener; tiltak av spredning, slik som standardavvik og variasjonskoeffisient kan også beregnes fra forholdet skalaer.

Sammendrag
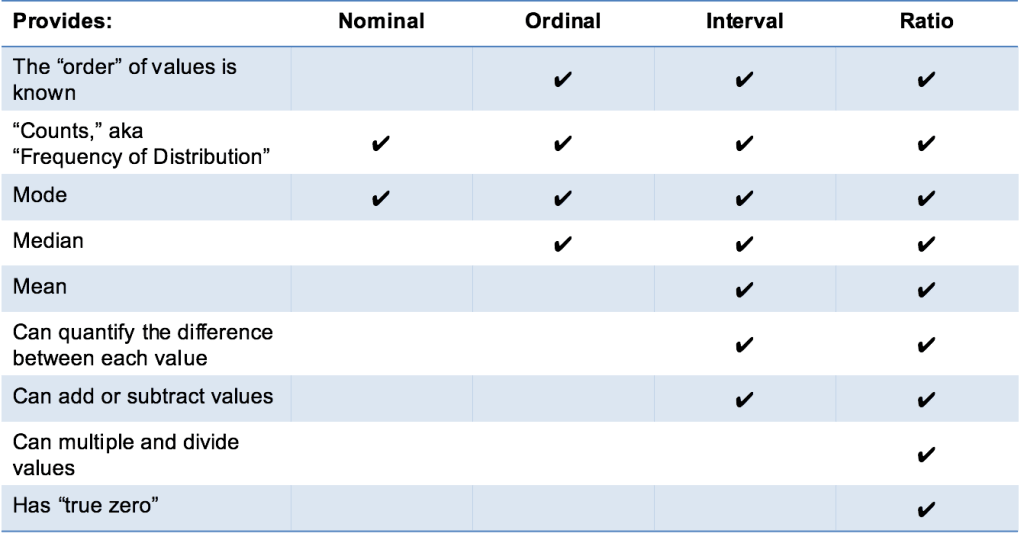
Det er det! Jeg håper denne forklaringen er klar, og at du vet forstår de fire typer data måling skalaer: nominell, ordinær, intervall, og ratio! Hent dem!
hvis du ønsker å teste dine ferdigheter, gi kort quiz under en gå(ikke fungerer ? Prøv på en stasjonær nettleser):