standardfeilen til gjennomsnittet, eller ganske enkelt standardfeilen, indikerer hvor forskjellig populasjonsgjennomsnittet sannsynligvis vil være fra et utvalgsgjennomsnitt. Den forteller deg hvor mye prøven mener vil variere hvis du skulle gjenta en studie ved hjelp av nye prøver fra en enkelt populasjon.
standardfeilen for gjennomsnittet (SE eller SEM) er den mest rapporterte typen standardfeil. Men du kan også finne standardfeilen for annen statistikk, som medianer eller proporsjoner. Standardfeilen er et vanlig mål for utvalgsfeil-forskjellen mellom en populasjonsparameter og en utvalgsstatistikk.
hvorfor standardfeil teller
i statistikk brukes data fra prøver til å forstå større populasjoner. Standardfeil er viktig fordi det hjelper deg med å anslå hvor godt eksempeldataene representerer hele populasjonen.
med sannsynlighetsutvalg, der elementer i et utvalg er tilfeldig valgt, kan du samle inn data som sannsynligvis er representative for populasjonen. Men selv med sannsynlighetsprøver, vil noen prøvetakingsfeil forbli. Det er fordi et utvalg aldri vil passe perfekt til befolkningen det kommer fra når det gjelder tiltak som midler og standardavvik.
ved å beregne standardfeil kan du anslå hvor representativt utvalget ditt er av populasjonen din og trekke gyldige konklusjoner.
en feil med høy standard viser at utvalgsmidler er bredt spredt rundt populasjonsgjennomsnittet-utvalget ditt representerer kanskje ikke populasjonen din. En lav standardfeil viser at utvalgsmidlene er tett fordelt rundt populasjonsgjennomsnittet-utvalget ditt er representativt for populasjonen din.
du kan redusere standardfeil ved å øke prøvestørrelsen. Ved hjelp av en stor, tilfeldig prøve er den beste måten å minimere sampling bias.
Standardfeil vs standardavvik
Standardfeil og standardavvik er begge mål på variabilitet:
- standardavviket beskriver variabilitet innenfor en enkelt prøve.
- standardfeilen anslår variabiliteten på tvers av flere prøver av en populasjon.


standardavviket er en beskrivende statistikk som kan beregnes ut fra eksempeldata. I kontrast er standardfeilen en inferensiell statistikk som bare kan estimeres (med mindre den virkelige populasjonsparameteren er kjent).
standardavviket for matematikkpoengene er 180. Dette tallet gjenspeiler i gjennomsnitt hvor mye hver poengsum er forskjellig fra utvalgsgjennomsnittet på 550.
standardfeilen til matematikkpoengene, derimot, forteller deg hvor mye utvalgsgjennomsnittet på 550 skiller seg fra andre utvalgsgjennomsnittpoeng, i prøver av samme størrelse, i populasjonen av alle testtakere i regionen.
standardfeilformel
standardfeilen til gjennomsnittet beregnes ved hjelp av standardavviket og prøvestørrelsen.
fra formelen ser du at prøvestørrelsen er omvendt proporsjonal med standardfeilen. Dette betyr at jo større prøven er, desto mindre er standardfeilen, fordi utvalgsstatistikken vil være nærmere å nærme seg populasjonsparameteren.
Ulike formler brukes avhengig av om populasjonsstandardavviket er kjent. Disse formlene fungerer for prøver med mer enn 20 elementer (n > 20).
når populasjonsparametere er kjent
når populasjonsstandardavviket er kjent, kan du bruke det i formelen nedenfor til å beregne standardfeil nøyaktig.
| Formel | Forklaring |
|---|---|
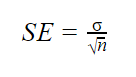 |
|
når populasjonsparametere er ukjente
når populasjonsstandardavviket er ukjent, kan du bruke formelen nedenfor til bare å estimere standardfeil. Denne formelen tar standardavviket som et punktestimat for populasjonsstandardavviket.
| Formel | Forklaring |
|---|---|
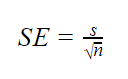 |
|
finn først kvadratroten av prøvestørrelsen (n).
| Formel | Beregning |
|---|---|
| √n | n = 200
√= √200 = 14.1 |
deretter deler du standardavviket med nummeret du fant i trinn ett.
| Formel | Beregning |
|---|---|
| SE = s ÷ √ n | s = 180
√n = 14,1 s ÷ √ = 180 ÷ 14.1 = 12.8 |
standard feil av matte SAT score er 12.8.
hvordan skal du rapportere standardfeilen?
du kan rapportere standardfeilen sammen med gjennomsnittet eller i et konfidensintervall for å kommunisere usikkerheten rundt gjennomsnittet.
den beste måten å rapportere standardfeilen på er i et konfidensintervall fordi leserne ikke trenger å gjøre noen ekstra matte for å komme opp med et meningsfylt intervall.
et konfidensintervall er en rekke verdier der en ukjent populasjonsparameter forventes å ligge mesteparten av tiden, hvis du skulle gjenta studien med nye tilfeldige prøver.
med et 95% konfidensnivå vil 95% av alle utvalgsmidler forventes å ligge innenfor et konfidensintervall på ± 1,96 standardfeil i utvalgsgjennomsnittet.
basert på tilfeldig prøvetaking, anslås også den sanne populasjonsparameteren å ligge innenfor dette området med 95% konfidens.
for en normalfordelt karakteristikk, som SAT-score, faller 95% av alle utvalgsmidler innenfor omtrent 4 standardfeil i utvalgsgjennomsnittet.
| Konfidensintervall formel | |
|---|---|
|
CI = x ± (1.96 × SE) x = eksempel gjennomsnitt = 550 |
|
| Nedre grense | Øvre grense |
|
x – (1.96 × SE) 550 − (1.96 × 12.8) = 525 |
x + (1.96 × SE) 550 + (1.96 × 12.8) = 575 |
ved tilfeldig prøvetaking forteller et 95% KI deg at det er 0,95 sannsynlighet for at populasjonens gjennomsnittlige matte-SAT-score er mellom 525 og 575.
Andre standardfeil
Bortsett fra standardfeilen til gjennomsnittet (og annen statistikk), er det to andre standardfeil du kan komme over: standardfeilen til estimatet og standardfeilen til måling.
standardfeilen til estimatet er relatert til regresjonsanalyse. Dette gjenspeiler variabiliteten rundt den estimerte regresjonslinjen og nøyaktigheten av regresjonsmodellen. Ved hjelp av standardfeilen i estimatet kan du konstruere et konfidensintervall for den sanne regresjonskoeffisienten.
standardfeilen for måling handler om påliteligheten til et mål. Det indikerer hvor variabel målefeilen til en test er, og det rapporteres ofte i standardisert testing. Standardfeilen for måling kan brukes til å skape et konfidensintervall for den sanne poengsummen til et element eller et individ.
Vanlige spørsmål om standardfeil
standardfeilen til gjennomsnittet, eller ganske enkelt standardfeilen, indikerer hvor forskjellig populasjonsgjennomsnittet sannsynligvis vil være fra et utvalgsgjennomsnitt. Den forteller deg hvor mye prøven mener vil variere hvis du skulle gjenta en studie ved hjelp av nye prøver fra en enkelt populasjon.
Standardfeil og standardavvik er begge mål på variabilitet. Standardavviket reflekterer variabilitet i et utvalg, mens standardfeilen anslår variabiliteten på tvers av prøver av en populasjon.
ved hjelp av beskrivende og inferensiell statistikk kan du lage to typer estimater om befolkningen: punktestimater og intervallestimater.
- et punktestimat er et enkelt verdiestimat for en parameter. For eksempel er et utvalgsgjennomsnitt et punktestimat av et populasjonsgjennomsnitt.
- et intervallestimat gir deg et verdiområde der parameteren forventes å ligge. Et konfidensintervall er den vanligste typen intervallestimat.
Begge typer estimater er viktige for å samle en klar ide om hvor en parameter sannsynligvis vil ligge.
