Hvordan Beregne P-Verdi i Excel?

Innhold

1. 1. Hva Er P-Verdien?
   2. Hvorfor Trenger Vi P-Verdien?
   3. Hvor Bruker Vi P-Verdien I Det Virkelige Liv?
      • Markedsføring
      • Sannsynlighet
   4. Hvordan Beregne P-Verdien i Excel?
   5. SISTE ORD

Hva er P-Verdien?

P-verdi Er et statistisk begrep som hjelper deg med å bestemme, hvis hypotesen du bruker er sant, sannsynligheten for utvalgsvariasjonen. Det forteller oss bare hva som er oddsen for å få disse resultatene hvis vår nullhypotese er sant.

• en nullhypotese er en hypotese som hevder at resultatene vi får er forårsaket av ren flaks.
• en alternativ hypotese hevder at resultatene vi får ikke er flaks, men det er ytre elementer som påvirker resultatene våre.

det er et svært viktig og vanlig brukt statistisk begrep og kan enkelt beregnes i dataanalyseprogrammer som Microsoft Excel. I denne artikkelen lærer du hvordan vi bruker det, hvor bruker vi det og hvordan kan vi beregne Det I Excel på ulike måter.

La oss begynne!

Hvorfor Trenger Vi P-Verdien?

mens du gjør forskning med store populasjoner, må du beregne statistikken for hver enkelt person. Men selv i et slikt tilfelle kan du ikke være sikker på om noe skjedde på grunn av tilfeldighet eller bare flaks, siden det er umulig å observere alt. Det er her statistikken kommer inn.

Statistiske beregninger kan ikke gi deg en absolutt sannhet, men de vil hjelpe deg med å få en god ide om dine undersøkelser.

P-verdi tillater oss å teste hypotesen om vårt emne. Vi kan sammenligne de matematiske resultatene med disse hypotesene og revurdere vår vei uten å bruke mye tid på forskning.

Hvor Bruker Vi P-Verdien I Det Virkelige Liv?

vi bruker sannsynlighetsverdien der vi prøver å teste en hypotese. Det kan være om forskning eller en enkel innsats vi gjorde med vår venn.

det er lettere å forstå det med eksempler.

Markedsføring:

La oss si at du jobber innenfor markedsføringsområdet, og ditt siste prosjekt er på kornannonsering.

Du har produsert en video for sosiale medier, og du har fått informasjonen for ganske brukere hoppet over den eller så på den i lang tid.

som et eksempel er den vanlige visningstiden for videoen 20 sekunder. Gjennomsnittet er 20 sekunder. Og du tok beslutningen om å redigere videoen med en del av mer gledelig musikk.

nå hvordan vil du gjenkjenne om det fungerte? På dette punktet bruker vi signifikansstatistikk.

først produserer du en nullhypotese:

en nullhypotese hevder at det ikke er noen sammenheng mellom hva du investerer og resultatene du får. Det påvirker ikke resultatene.

under dette eksemplet vil nullhypotesen være dette: «Det er ikke noe forhold mellom endringene du søker på klokken.»

så den alternative hypotesen:

den alternative hypotesen antyder at faktisk endring av musikken fungerte og nå ser folk på reklamen i mer enn 20 sekunder. Matematisk sier den alternative hypotesen:

» gjennomsnittet er større enn 20 sekunder nå.»

Beregn Signifikansnivået:

nå må Vi sette en grenseterskel for å beregne om vi lykkes eller ikke. Dette kalles et signifikansnivå er også referert til som alfa-verdien. Det kan være hvilken som helst prosentandel du vil, det er helt opp til deg.

men i dette eksemplet vil det være 0,05.

nå for å beregne med sikkerhet, bør vi alltid ha alle dataene på klokken. Men når det gjelder tid og kilder, bør du ta et utvalg fra befolkningen:

1. Du tok et utvalg av 100 personer.
2. Disse 100 personer har 25 sekunder av watch tid for den kommersielle.
3. det betyr at utvalgsgjennomsnittet er 25.

dette er en veldig enkel versjon av beregningen. Men standardavviket for prøven beregnes vanligvis i denne skalaen hvis du ikke vet standardavviket for hele befolkningen.

du kan bruke verdiene du har beregnet for utvalget, siden de er nær populasjonsverdiene. Utvalgsgjennomsnittet er nær populasjonsgjennomsnittet.

Beregn P-Verdien:

p-verdien viser oss om vi kan avvise nullhypotesen eller ikke. Sannsynligheten for at utvalgsgjennomsnittet er større enn eller lik 25 minutter gitt nullhypotesen, er sant.

det er to situasjoner som kan skje.

1. hvis p-verdien er mindre enn alfa, kan du avvise nullhypotesen. Du har fått statistisk bevis på at den alternative hypotesen er sant.
2. Men hvis p-verdien er større eller lik alfa, kan du ikke avvise nullhypotesen. Det betyr ikke at nullhypotesen er sikkert sant, men det kan heller ikke unngås.

Sannsynlighet

la oss jobbe med et annet eksempel.

din venn og du gjorde kaste mynt i luften: hvis det er haler du mister 5 dollar og hvis det kommer hoder du får 5 dollar.

• din venn knipser mynten en gang: den kommer som haler. Det er greit, det er en 50% sjanse for at det kommer som haler. Na antar du sannsynligheten er 0,5 fordi du tror det er en rettferdig mynt. Dette er din nullhypotese.

• Andre: det er haler. Du mistet en annen 5 dollar, men det er greit fordi det fortsatt er en god sjanse for to haler på rad. P-verdien er 0,25 og det er fortsatt et rettferdig forhold.
• Tredje: det er haler igjen. Sjansen for haler tre ganger pa rad er 0,12. Det er ikke lavt, så det er ikke nok bevis på at nullhypotesen ikke er riktig. Men du begynner å tenke at din alternative hypotese kan være riktig.
• Fjerde: Det blir som haler igjen, du vil se hvordan sjansene blir veldig lave. Det kan være en mirakuløs tilfeldighet, men det er fortsatt en 0,6 sjanse, og det er fortsatt ikke nok bevis for å støtte den alternative hypotesen som sier at mynten er vanskelig. Og du venter på den femte flippen.
• Femte: det er haler. Sjansen for en mynt viser seg som haler fem ganger pa rad er 0,3 som er veldig lav. Dette er poenget du kan avvise nullhypotesen for det er ikke nok bevis for å støtte det lenger.

du spør vennen din om å se mynten, og når du holder den, skjønner du at den har to haler og det er en vanskelig mynt.

hva fikk oss til å miste troen på vår nullhypotese?

i et rettferdig spill med å bla mynter, er sjansen for å få en krone eller en mynt 50%. Dette er en situasjon der vi tror mynten er rettferdig, men som p-verdien faller vår tillit til den hypotesen svekket også.

det er liten sjanse for å ha tilfeldige haler når p-verdien faller under 0,05. Så når du bruker denne statistiske termen på saker som kreftforskning eller effekter av klimaendringer, blir det viktigere.

 Merk: det er ingen spesiell grunn til at vi bruker 0,05 p-verdi for standardberegning. Skaperen av formelen bestemte seg for at det var et godt tall for beregning og standardberegningene holder seg til det. 0,05 betyr 5% i 100 individer populasjoner som faller inn i den normale kurven. Dette er en av grunnene til at det ofte brukes. Hvis du vil endre det under beregning av det selv, kan du.

Hvordan Beregne P-Verdien i Excel?

det er mer enn en måte å beregne p-verdien på I Microsoft Excel. Du kan skrive ned formler, eller du kan bruke Analyseverktøy. Denne artikkelen inneholder hvordan du gjør det begge veier.

Bruk Av Klassiske Excel-Formler:

la oss starte med den klassiske Excel-formelveien. Det er to måter å gjøre DETTE tdist formel Og T-test formel.

1.1) TFORDELINGSFORMEL

Først av Alt trenger du et datasett for å beregne en p-verdi.

• la oss si at du er lærer, Og du vil sammenligne hva elevene dine scoret i din siste eksamen og hva du forventet at poengsummen var basert på tidligere eksamener.
• du har resultatene 25, 46, 34, 27, 35, 43, 40, 44, 21 og 39 for din siste eksamen.
• nå for beregning, trenger du en annen hale, dette er poengsummen du forventet basert på tidligere tester: 23, 44, 32, 20, 46, 37, 35, 42, 33, og 35

Nå, for å kunne bruke p-verdi formelen På Excel, bør du beregne noen ting på forhånd:

Pearson koeffisient (r): Det er et statistisk begrep som måler den lineære korrelasjonen mellom to data. Du trenger ikke å vite det matematiske aspektet av det for å beregne p-verdien. Du vil se den enkle formelen for det i de neste avsnittene.

Befolkning (n): n er det totale antallet individer i datasettet.

t statistikk: det er forholdet mellom avviket av data estimert verdi fra antatt verdi til standardfeil.

grad av frihet: det er antall individer i datasettet minus to.

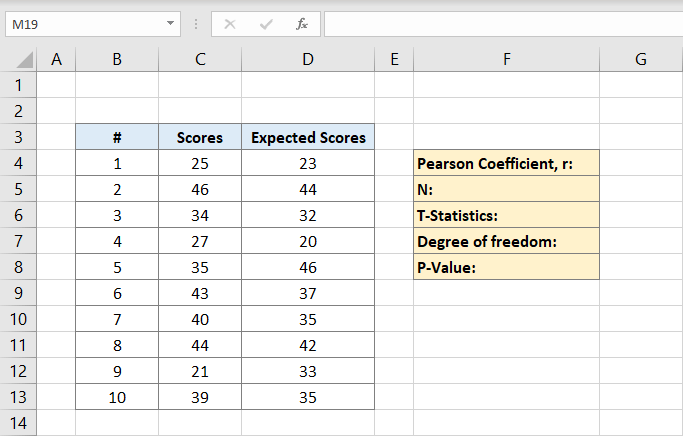
Nå Vil Pearson-koeffisienten bli skrevet På F4 i dette eksemplet. Etter at du har klikket på det, skriver du inn formelen:

C-kolonnene er for poengene og D-kolonnene er for de forventede poengene. Pearson-koeffisienten er 0,691473 i dette eksemplet.

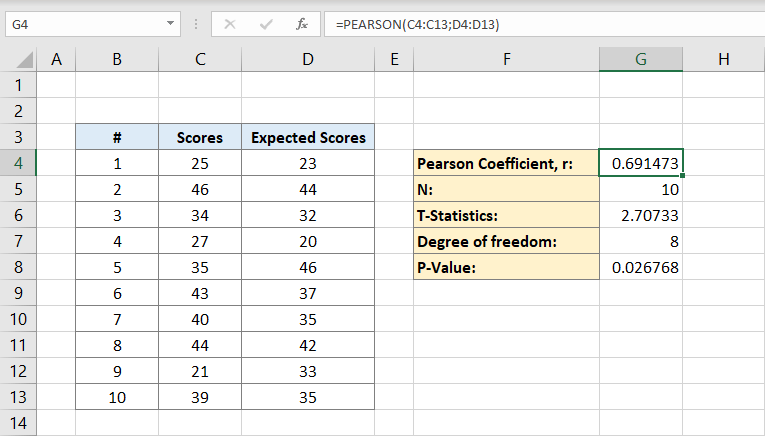
Deretter skriver du inn antall personer i datasettet. Hvis du vet sikkert hvor mange personer du har, kan du skrive det manuelt, men hvis du ikke gjør det, kan du bruke formelen:

hvorfor inneholder formelen bare en c-kolonne?

det er fordi vi bare trenger enkeltpersoner i ett datasett for å beregne derfor en kolonne vil gjøre. Cellen G5 vil nå inneholde tallet 10 i den. Dette er vår befolkning.

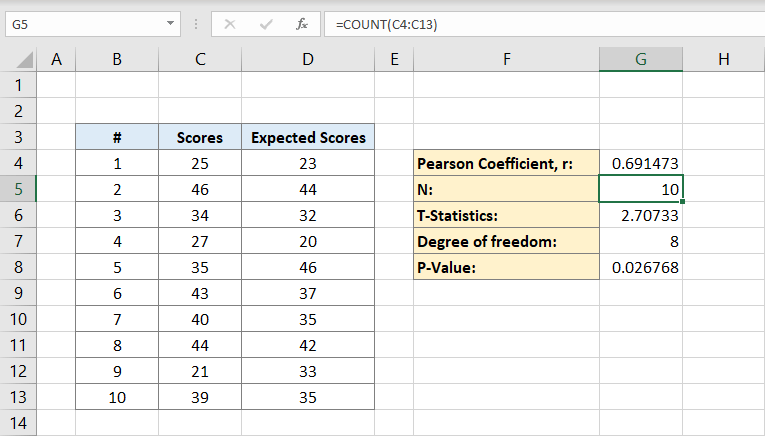
Nå som du har Både Pearson-koeffisienten og befolkningen, kan Du beregne t-statistikk. Den matematiske formelen For t statistikk Er Pearson koeffisient (r) ganger tegn kvadratroten av befolkningen (n) minus 2 dividert med kvadratroten av 1 minus Pearson koeffisient kvadrat:

Cellen G6 vil inneholde resultatet 2,70733. Dette er Vår t statistikk.

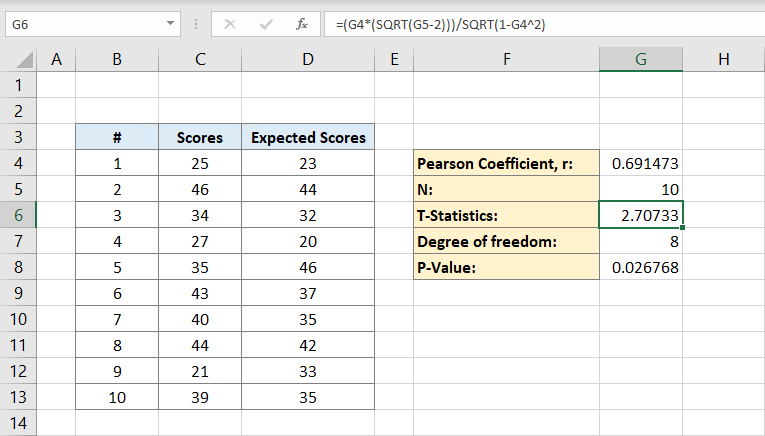
Etter det vil du beregne graden av frihet. Du vil skrive:

til cellen G7. Dette er graden av frihet. Det vil være på 8.

Nå har du alt du trenger for å beregne p-verdien. Cellen G8 vil inneholde formelen for den. Det er:

Eller

resultatet blir 0,026768. Dette er p-verdien for datasettet.

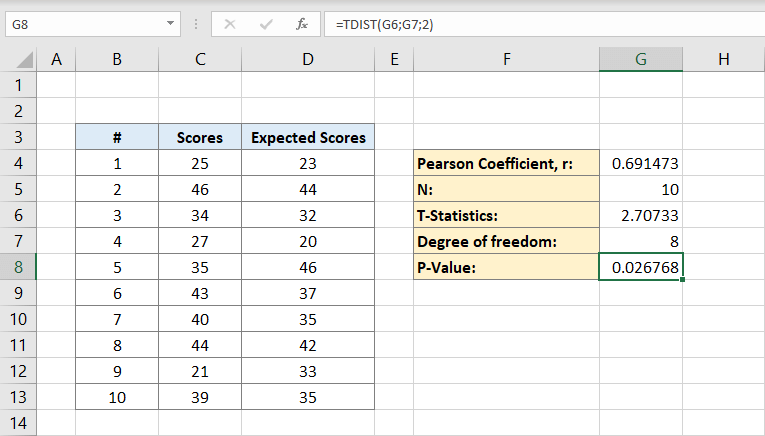
1.2. T-Test Formel

den andre måten å bestemme p-verdien med Excel-formler, bruker t-test-formelen. Det er litt lik forrige eksempel, men kortere.

• La oss si at datasettet er det samme, du har resultatene 25, 46, 34, 27, 35,43, 40, 44, 21, 39 for din siste eksamen.
• Forventede resultater er 23, 44, 32, 20, 46, 37, 35, 42, 33, 35.
• du skal legge til en tredje kolonne for forskjellen mellom det som var forventet og den faktiske poengsummen. I differansekolonnen 2, 2, 2, 7, 11, 6, 5, 2, 12, 4 vil bli skrevet Fra E4 Til E13.

skriv Nå T-Test til cellen E8. Du skal skrive t-testformelen til den tomme cellen ved siden av den. Det er:

og denne formelen vil gi deg p-verdien direkte.

Bestem P-Verdien Med Excel-Verktøyet Pak

Tok Pak er en pakke som lar deg beregne ulike statistiske målinger automatisk, slik at det er enkelt og veldig praktisk. Det er også enkelt å installere.

Trinn 1: Gå til innstillinger. Det er en» Add-ins » – knapp nederst i venstre hjørne, klikk på den. Et nytt vindu vises, finn alternativet «Analyseverktøy Pak», klikk på det, og klikk deretter på go-knappen nederst i vinduet.

Trinn 2: Aktiver tillegget ved å klikke på krysssymbolet ved siden av DET og ETTER OK-knappen i høyre kolonne.

Trinn 3: hvis du klarte å aktivere det riktig, vises en» Data analysis » – knapp på toppmenyen i regnearket til høyre side.

Trinn 4: Klikk på» Data analysis «- knappen og velg» t-Test: Paired Two Sample For Means » – alternativet. Klikk OK etter det. Et nytt vindu vil vises.

Trinn 5: det vil spørre inngangene i den første raden i vinduet. Skriv C4: C13 til boksen» variable 1 range». Du vil skrive D4: D13 til boksen» variable 2 range». La alfa-boksen stå med standardverdien.

Trinn 6: i den andre raden i vinduet kan du velge hvor du vil overvåke resultatene. Det kan være et nytt regneark eller noen tomme celler. Hvis du vil at resultatet på en celle må du låse kolonnen og raden. Klikk PÅ OK-knappen etter det.

 Tips: Bruk dollartegnet før bokstaven og nummeret for å låse kolonnen og raden. Hvis Du for eksempel vil låse a2-celle, skriver du inn $a$2.

Trinn 7: Excel vil beregne gjennomsnitt, varians, observasjoner, Pearson korrelasjon, hypotese gjennomsnittlig forskjell, t statistikk, p-verdi, og mer.

SISTE ORD

P-verdien er enkel å beregne og tilpasse i mange ulike situasjoner. Det hjelper deg å få den informasjonen du trenger uten å bruke mye tid eller krefter på det. Det er enda enklere å beregne når du bruker statistiske analyseprogrammer Som Microsoft Excel som kommer med de riktige verktøyene og formlene. La oss sjekke someka maler samling og laste ned statistiske maler for å gjøre jobben enklere!

Relaterte Avlesninger:

• Hvordan Beregne Konfidensintervall I Excel?
• Kan Excel Analysere Data?