平均の標準誤差、または単に標準誤差は、母集団平均が標本平均とどのように異なる可能性があるかを示します。 単一の母集団内の新しいサンプルを使用して調査を繰り返す場合、サンプル平均がどのくらい変化するかがわかります。
平均の標準誤差(SEまたはSEM)は、最も一般的に報告されるタイプの標準誤差です。 しかし、中央値や比率など、他の統計の標準誤差を見つけることもできます。 標準誤差は、母集団パラメータと標本統計量の差である標本誤差の一般的な尺度です。
標準誤差が重要な理由
統計では、サンプルからのデータは、より大きな母集団を理解するために使用されます。 標準誤差は、サンプルデータが母集団全体をどの程度うまく表しているかを推定するのに役立つためです。
サンプルの要素をランダムに選択する確率サンプリングを使用すると、母集団を代表する可能性の高いデータを収集できます。 しかし、確率サンプルであっても、いくつかのサンプリング誤差が残ります。 これは、平均や標準偏差などの尺度に関して、サンプルが由来する母集団と完全に一致することは決してないためです。
標準誤差を計算することにより、サンプルが母集団のどのように代表的であるかを推定し、有効な結論を出すことができます。
高い標準誤差は、標本平均が母集団平均の周りに広く分布していることを示しています—あなたの標本はあなたの母集団を厳密に表していない可 低い標準誤差は、標本平均が母平均の周りに密接に分布していることを示しています—あなたの標本はあなたの母集団を代表しています。
サンプルサイズを増やすことで標準誤差を減らすことができます。 サンプリングバイアスを最小化するには、大きなランダムサンプルを使用するのが最善の方法です。
標準誤差と標準偏差
標準誤差と標準偏差はどちらも変動性の尺度です:
- 標準偏差は、単一のサンプル内の変動性を表します。
- 標準誤差は、母集団の複数のサンプルにわたる変動性を推定します。


標準偏差は、サンプルデータから計算できる記述統計量です。 対照的に、標準誤差は推定のみ可能な推論統計量です(実際の母集団パラメータが既知でない限り)。
数学のスコアの標準偏差は180です。 この数値は、各スコアが550のサンプル平均スコアとどの程度異なるかを平均して反映します。
一方、数学のスコアの標準誤差は、550のサンプル平均スコアが、地域内のすべての受験者の母集団において、同じサイズのサンプルで、他のサンプル平均スコアとどのくらい異なるかを示しています。
標準誤差式
平均の標準誤差は、標準偏差とサンプルサイズを使用して計算されます。
式から、サンプルサイズは標準誤差に反比例していることがわかります。 これは、標本統計量が母集団パラメーターに近づくほど、標本が大きいほど標準誤差が小さくなることを意味します。
母集団の標準偏差がわかっているかどうかに応じて、異なる式が使用されます。 これらの式は、20以上の要素(n>20)を持つサンプルに対して機能します。
母集団パラメータがわかっている場合
母集団標準偏差がわかっている場合は、以下の式で標準誤差を正確に計算することができます。
| 数式 | 説明 |
|---|---|
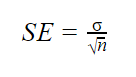 |
|
母集団パラメータが不明な場合
母集団の標準偏差が不明な場合は、以下の式を使用して標準誤差のみを推定できます。 この式は、標本標準偏差を母集団標準偏差の点推定値として取ります。
| 数式 | 説明 |
|---|---|
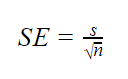 |
|
まず、サンプルサイズ(n)の平方根を求めます。
| 数式 | 計算 |
|---|---|
| √n | n=200
≤n= √200 = 14.1 |
次に、サンプル標準偏差をステップ1で見つけた数で除算します。
| 数式 | 計算 |
|---|---|
| SE=s÷√n | s=180
√n=14.1 s÷√n= 180 ÷ 14.1 = 12.8 |
数学のSATスコアの標準誤差は12.8です。
どのように標準エラーを報告する必要がありますか?
標準誤差を平均値と一緒に報告するか、信頼区間で報告して、平均値の不確実性を伝えることができます。
標準誤差を報告する最良の方法は、読者が意味のある間隔を考え出すために追加の数学を行う必要がないため、信頼区間にあります。
信頼区間とは、新しいランダムサンプルで調査を繰り返す場合、未知の母集団パラメータがほとんどの場合存在すると予想される値の範囲です。
95%の信頼水準では、すべての標本平均の95%が標本平均の±1.96標準誤差の信頼区間内にあると予想されます。
無作為抽出に基づいて、真の母集団パラメータも95%の信頼度でこの範囲内にあると推定されます。
SATスコアのような正規分布特性では、すべての標本平均の95%が標本平均の約4つの標準誤差の範囲内に入る。
| 信頼区間の式 | |
|---|---|
|
CI=x±(1.96×SE) x=サンプル平均=550 |
|
| 下限 | 上限 |
|
x−(1.96×セ) 550 − (1.96 × 12.8) = 525 |
×+(1.96×)) 550 + (1.96 × 12.8) = 575 |
無作為抽出では、95%CIは、母集団平均数学SATスコアが525と575の間であることを0.95確率があることを示しています。
その他の標準誤差
平均(およびその他の統計)の標準誤差とは別に、推定値の標準誤差と測定値の標準誤差という二つの標準誤差があります。
推定値の標準誤差は回帰分析に関連しています。 これは、推定された回帰線の周りの変動性と回帰モデルの精度を反映しています。 推定値の標準誤差を使用して、真の回帰係数の信頼区間を構築できます。
測定の標準誤差は、測定の信頼性に関するものです。 これは、テストの測定誤差がどのように可変であるかを示し、それは多くの場合、標準化されたテストで報告されています。 測定の標準誤差は、要素または個人の真のスコアの信頼区間を作成するために使用することができます。
標準エラーに関するよくある質問
平均の標準誤差、または単に標準誤差は、母集団平均が標本平均とどの程度異なるかを示します。 単一の母集団内の新しいサンプルを使用して調査を繰り返す場合、サンプル平均がどのくらい変化するかがわかります。
標準誤差と標準偏差はどちらも変動性の尺度です。 標準偏差は標本内の変動性を反映し、標準誤差は母集団の標本間の変動性を推定します。
記述統計と推論統計を使用して、母集団についての2つのタイプの推定を行うことができます:点推定値と区間推定値。
- ポイント推定値は、パラメータの単一値推定値です。 たとえば、標本平均は母集団平均の点推定値です。
- 間隔の推定値は、パラメータが存在すると予想される値の範囲を与えます。 信頼区間は、区間推定の最も一般的なタイプです。
両方のタイプの推定値は、パラメータがどこにある可能性があるかの明確なアイデアを収集するために重要です。
