統計には、公称、順序、間隔および比率の四つのデー これらは、さまざまなタイプのデータをサブ分類するための単純な方法です(統計データタイプの概要は次のとおりです)。 このトピックは、通常、学術教育の文脈で議論され、”現実の世界”ではあまり頻繁に議論されません。「統計テストのためにこの概念をブラッシュアップしている場合は、これらの用語を思いついたStanley Stevensという心理学者の研究者に感謝します。
これらの四つのデータ測定スケール(公称、順序、間隔、および比)は、以下に示すように、例で最もよく理解されています。
公称スケールは、定量的な値なしで、変数をラベル付けするために使用されます。 “公称”スケールは、単に”ラベル”と呼ばれることができます。”ここでは、以下のいくつかの例があります。 これらのスケールはすべて相互に排他的であり(重複はありません)、数値的に重要な意味を持つものはありません。 このすべてを覚えておくのに良い方法は、「公称」は「名前」のように聞こえ、公称スケールは「名前」やラベルのようなものです。
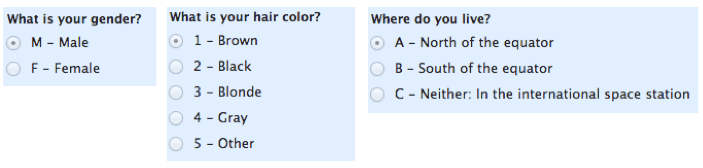
注:二つのカテゴリ(例えば、男性/女性)のみを持つ公称スケールのサブタイプは、”二分法”と呼ばれます。”あなたが学生であれば、あなたの先生を感動させるためにそれを使用することができます。
ボーナスノート#2: 他のサブタイプの公称データは、「注文のある公称」(「冷たい、暖かい、熱い、非常に熱い」など)および注文のない公称(「男性/女性」など)です。
序数
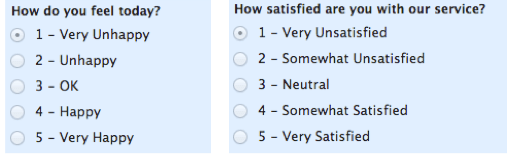
序数スケールでは、値の順序が重要で重要ですが、それぞれの違いは実際にはわかりません。 以下の例を見てみましょう。 いずれの場合も、A#4がA#3または#2よりも優れていることはわかっていますが、それがどれほど優れているかはわかりませんし、定量化できません。 たとえば、「OK」と「不幸」の違いは、「非常に幸せ」と「幸せ」の違いと同じですか?「……………………………」
序数スケールは、通常、満足度、幸福、不快感などの非数値概念の尺度です。
“序数”は”順序”のように聞こえるので覚えやすいですし、それが”序数スケール”で覚えておくべき鍵です–それは重要な順序ですが、それはあなたが本当にこ
高度な注意:順序データのセットの中心傾向を決定するための最良の方法は、モードまたは中央値を使用することです。
間隔
間隔スケールは、値の順序と正確な違いの両方を知っている数値スケールです。 間隔スケールの典型的な例は、各値の差が同じであるため、摂氏温度です。 例えば、60度と50度の差は測定可能な10度であり、80度と70度の差は測定可能な10度である。
間隔スケールは、これらのデータセットの統計分析の領域が開くので素晴らしいです。 例えば、中心傾向は、モード、中央値、または平均によって測定することができ、標準偏差も計算することができる。
他の人と同じように、”間隔スケール”の重要なポイントをかなり簡単に覚えておくことができます。 “間隔”自体は、覚えておくべき重要なことである”間のスペース”を意味します–間隔スケールは、順序についてだけでなく、各項目間の値についても教えてくださ
ここに間隔スケールの問題があります:彼らは”真のゼロを持っていません。「たとえば、「温度なし」のようなものは、少なくとも摂氏ではありません。 間隔スケールの場合、ゼロは値がないことを意味するものではありませんが、実際には摂氏0度のようにスケールで使用される別の数値です。 負の数にも意味があります。 真のゼロがなければ、比率を計算することは不可能です。 区間データでは、加算と減算はできますが、乗算または除算はできません。
Ok、これを考慮してください:10度C+10度C=20度c問題はありません。 それは摂氏スケールに来るとき”温度なし”のようなものはありませんので、しかし、20度Cは、10度Cの倍の高温ではありません。 華氏に変換すると、10C=50Fと20C=68Fは明らかに2倍の暑さではありません。 それが理にかなっていることを願っています。 一番下の行は、間隔スケールは素晴らしいですが、我々は私たちの最後の測定スケールに私たちをもたらす比率を計算することはできません…

比率
比率スケールは、順序について教えてくれるので、データ測定スケールに来るとき、彼らは私たちに単位間の正確な値を教えてくれる、と彼らはまた、絶対ゼロを持っている–これは、記述的および推論的な統計の広い範囲を適用することができます。 自分自身を繰り返す危険性があるため、区間データに関する上記のすべてが比率スケールに適用され、比率スケールにはゼロの明確な定義があります。 比率変数の良い例には、身長、体重、および持続時間が含まれます。
比率スケールは、統計分析に関して豊富な可能性を提供します。 これらの変数は、有意に加算、減算、乗算、分割(比率)することができます。 中心傾向は、モード、中央値、または平均によって測定することができ、標準偏差および変動係数などの分散の測定値は、比スケールからも計算することがで

要約
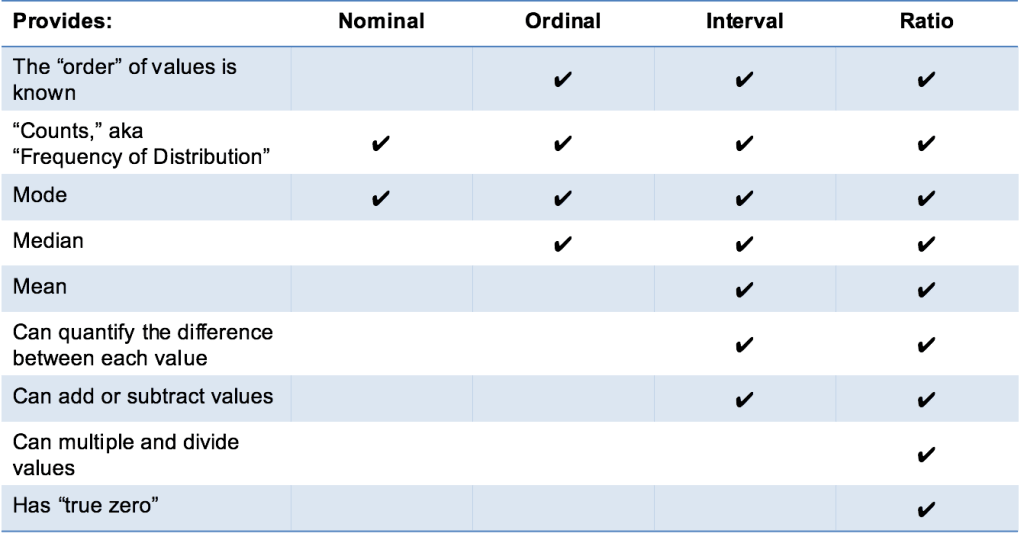
それだけです! 私はこの説明が明確であり、あなたが知っている4つのタイプのデータ測定スケールを理解していることを願っています:公称、順序、間隔、および比率! Emを捕まえろ!
あなたのスキルをテストしたい場合は、goの下の簡単なクイズを与えます(動作していませんか? デスクトップブラウザを試してみる):