-
- P値とは何ですか?
- なぜP値が必要なのですか?
- 実生活ではどこでP値を使うのですか?
- マーケティング
- 確率
- どのようにExcelでP値を計算するのですか?
P値とは何ですか?
P値は、使用する仮説が真であるかどうか、サンプリング変動の確率を決定するのに役立つ統計的な項です。 帰無仮説が真であれば、これらの結果を得る確率は何かを単純に示しています。帰無仮説は、私たちが得た結果が純粋な運によって引き起こされたと主張する仮説です。
これは非常に重要で一般的に使用される統計用語であり、Microsoft Excelのようなデータ分析プログラムで簡単に計算できます。 この記事では、どのように使用するのか、どこで使用するのか、さまざまな方法でExcelでどのように計算できるのかを学びます。
始めましょう!
なぜP値が必要なのですか?
大規模な集団で研究を行っている間は、各個人の統計を計算する必要があります。 しかし、そのような場合でも、すべてを観察することは不可能であるため、偶然のせいで何かが起こったのか、単に運のせいで何かが起こったのかは確 これが統計の出番です。
統計計算はあなたに絶対的な真実を与えることはできませんが、彼らはあなたの研究の良いアイデアを持つのに役立ちます。
P値は、私たちの主題に関する仮説を検定することを可能にします。 これらの仮説と数学的結果を比較し、研究に多大な時間を費やすことなく、私たちの道を再考することができます。
実際の生活の中でP値をどこで使用しますか?
仮説を検定しようとする確率値を使用します。 それは私達が私達の友人と作った研究か簡単な賭けについてある場合もある。
例で理解しやすい。
マーケティング:
あなたがマーケティング領域内で働いていて、最近のプロジェクトが穀物広告にあるとしましょう。
あなたはソーシャルメディアのためのビデオを制作しており、むしろユーザーのための情報を持っていますそれをスキップしたり、長い間それを見た。
一例として、ビデオの一般的な視聴時間は20秒です。 平均は20秒です。 そして、あなたはより楽しい音楽の塊でビデオを編集することを決定しました。
今、それが働いたかどうかをどのように認識しますか? この時点で、有意性統計を使用します。
まず、帰無仮説を生成します:
帰無仮説は、あなたが投資したものとあなたが得た結果との間に相関がないと主張しています。 結果には影響しません。
この例では、帰無仮説は次のようになります:”ウォッチ時間に適用している変更の間には関係がありません。”
そして、対立仮説:
対立仮説は、実際に音楽を変更することが働いたことを示唆しており、今では人々は20秒以上コマーシャルを見ています。 数学的には対立仮説は次のように述べています:
「今は平均値が20秒より大きい。”
有意水準を計算する:
ここで、成功したかどうかを計算するための境界しきい値を設定する必要があります。 これは有意水準と呼ばれ、さらにアルファ値と呼ばれます。 それはあなたが望む任意の割合をすることができます、それは絶対にあなた次第です。
しかし、この例では、0,05になります。
今、確実に計算するためには、常に時計時間のすべてのデータを持つ必要があります。 しかし、あなたの時間と情報源の面では、人口からサンプルを取る必要があります:
- あなたは100人のサンプルを取った。
- この100人はコマーシャルのために25秒の時計時間を持っています。
- これは、サンプル平均が25であることを意味します。
これは計算の非常に単純なバージョンです。 しかし、母集団全体の標準偏差がわからない場合、サンプルの標準偏差は通常このスケールで計算されます。
母集団値に近いため、サンプルに対して計算した値を使用できます。 標本平均は母集団平均に近いです。
:
p値は帰無仮説を棄却できるかどうかを示します。 帰無仮説を仮定すると、標本平均が25分以上である確率は真です。
発生する可能性のある状況は2つあります。
- p値がアルファより小さい場合、帰無仮説を棄却できます。 あなたは対立仮説が真であるという統計的証拠を持っています。
- しかし、p値がα以上の場合、帰無仮説を棄却することはできません。 それは帰無仮説が確かに真であることを意味するものではありませんが、それも避けることはできません。
確率
別の例に取り組んでみましょう。
あなたの友人とあなたは空中でコインを投げました:それは尾であれば、あなたは5ドルを失い、それが頭に来るならば、あなたは5ドルを得ます。
- あなたの友人は一度コインを反転します:それは尾として来ます。 それは大丈夫です、それが尾として来るという50%の確率があります。 今、あなたはそれが公正なコインであると信じているので、確率は0,5であると仮定します。 これは帰無仮説です。
- あなたは別の5ドルを失ったが、行の二つの尾の良いチャンスがまだあるので、それは大丈夫です。 P値は0,25であり、それはまだ公正な比率です。
- 第三:再び尾です。 連続して3回の尾のチャンスは0,12です。 それは低くないので、帰無仮説が正しくないという十分な証拠がありません。 しかし、あなたはあなたの対立仮説が正しいかもしれないと考え始めます。
- 第四:それは再び尾のようになりますあなたはチャンスが本当に低くなっている方法がわかります。 それは奇跡的な偶然かもしれませんが、まだ0,6のチャンスがあり、コインがトリッキーであると言う対立仮説を支持するのに十分な証拠がまだあ そして、あなたは第五のフリップを待ちます。
- 第五:それは尾です。 コインのチャンスは、行の尾が5回であるとして判明0,3これは非常に低いです. これは、それを支持するのに十分な証拠がないため、帰無仮説を棄却できる点です。

あなたはコインを見るためにあなたの友人に尋ね、あなたがそれを保持するとき、あなたはそれが二つの尾側を持っており、それはトリッキーなコ
帰無仮説に対する信頼を失う原因は何でしたか?
コインをめくる公正なゲームでは、頭や尾を得る確率は50%です。 これは、コインが公正であると信じている状況ですが、p値が低下するにつれて、その仮説に対する私たちの信頼も弱まりました。
p値が0,05を下回った場合、ランダムな裾を持つ可能性はほとんどありません。 したがって、この統計用語を癌研究や気候変動の影響などの問題に適用すると、より重要性が増します。
注:デフォルトの計算に0,05p-valueを使用する特別な理由はありません。 数式の作成者は、それが計算に適した数であり、デフォルトの計算がそれに固執すると判断しました。 0,05は、通常の曲線に分類される5人の人口の100%を意味します。 これは、それが一般的に使用されている理由の一つです。 自分で計算中に変更したい場合は、次のことができます。
ExcelでP値を計算するには?
Microsoft Excelでp値を計算するには、複数の方法があります。 数式を入力するか、分析ToolPakを使用できます。 この記事では、両方の方法でそれを行う方法が含まれています。
古典的なExcel式の使用:
古典的なExcel式の方法から始めましょう。 このTDIST式とT検定式を行うには、2つの方法があります。
1.1)TDIST式
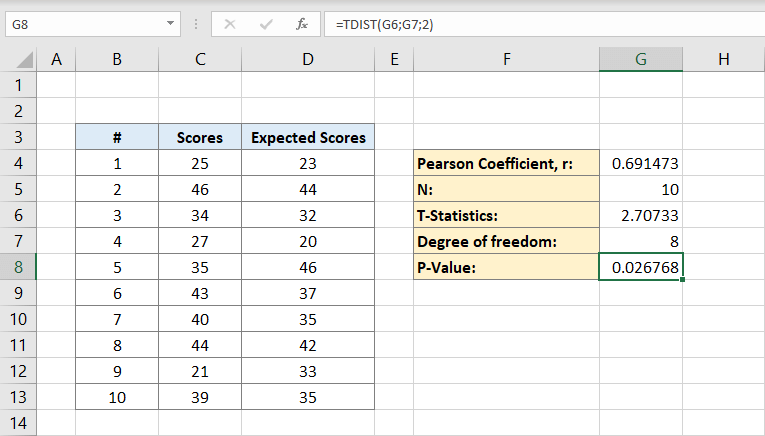
まず、p値を計算するためのデータセットが必要です。
- あなたが教師であり、あなたの学生があなたの最後の試験で得点したものと、以前の試験に基づいて彼らのスコアが期待されるものを比較したいとし
- あなたは結果を持っています25, 46, 34, 27, 35, 43, 40, 44, 21 そして、あなたの最新の試験のための39。
- 今計算のために、あなたは別の尾を必要とします、これはあなたが以前のテストに基づいて期待したスコアです: 23, 44, 32, 20, 46, 37, 35, 42, 33, と35
ここで、Excelでp値式を使用するには、事前にいくつかのことを計算する必要があります。
Pearson coefficient(r): これは、2つのデータ間の線形相関を測定する統計用語です。 あなたはp値を計算するためにそれの数学的側面を知る必要はありません。 次の段落で簡単な式が表示されます。
母集団(n):nはデータセット内の個人の総数です。
t統計量:データ推定値の想定値から標準誤差への偏差の比です。
自由度:データセット内の個体数から2を引いた値です。
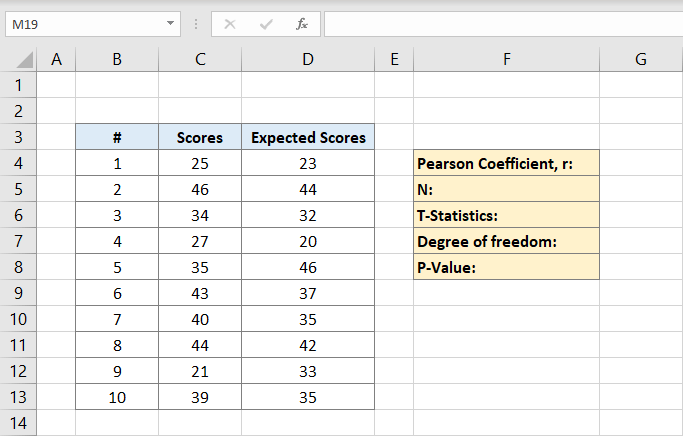
ここで、ピアソン係数はこの例ではF4に書き込まれます。 クリックした後、数式を入力します。
c列はスコア、D列は予想されるスコアです。 この例では、ピアソン係数は0,691473です。
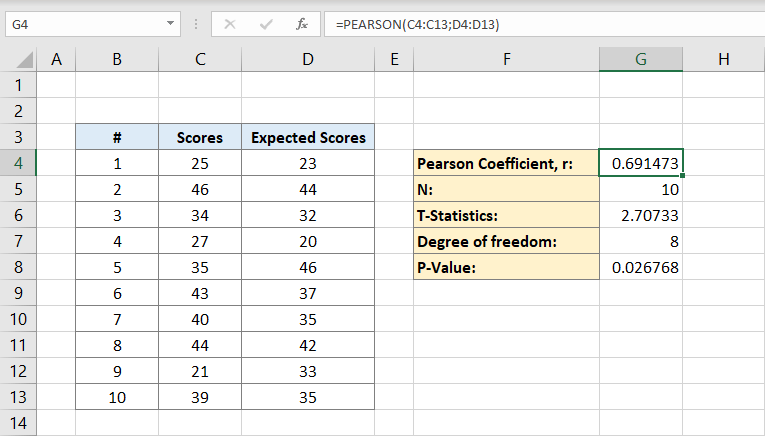
次に、データセット内の個人の数を入力します。 あなたが持っている個人の数を確かに知っていれば、手動で入力することができますが、そうでない場合は式を使用することができます:
数式にC列のみが含まれているのはなぜですか?
それは、計算するために1つのデータセットの個人だけが必要なため、1つの列が実行されるためです。 セルG5には10という数字が含まれます。 これは私たちの人口です。
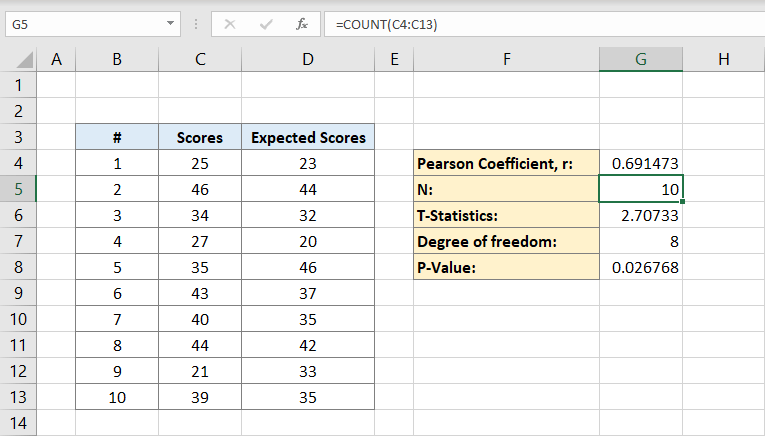
Pearson係数と母集団の両方が得られたので、T統計量を計算できます。 T統計の数式は、母集団(n)のピアソン係数(r)倍符号平方根マイナス2を1の平方根マイナスピアソン係数の二乗で割ったものです:
セルG6には結果2,70733が含まれます。 これは私たちのT統計です。
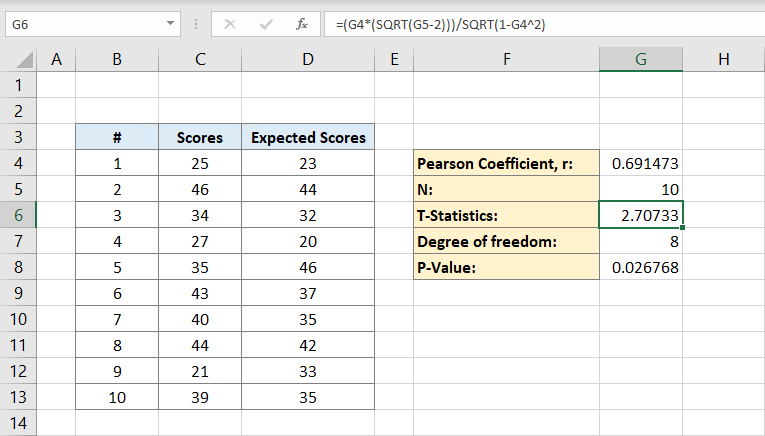
その後、自由度を計算します。 セルG7に
と入力します。 これが自由度です。 それは8になります。
これで、P値を計算するために必要なすべてが得られました。 セルG8には、その数式が含まれます。 つまり、
または
結果は0,026768になります。 これは、データセットのp値です。
1.2. T検定式
Excelの数式でp値を決定する2番目の方法は、T検定式を使用することです。 これは、前の例に少し似ていますが、短いです。
- データセットが同じであるとしましょう、あなたは結果を持っています25, 46, 34, 27, 35,43, 40, 44, 21, 39 あなたの最新の試験のために。
- 期待される結果は次のとおりです23, 44, 32, 20, 46, 37, 35, 42, 33, 35.
- 期待されたものと実際のスコアの差のための第三の列を追加しようとしています。 差分列で2, 2, 2, 7, 11, 6, 5, 2, 12, 4 e4からE13に書き込まれます。
ここで、セルE8にT-Testと入力します。 あなたはそれの隣の空白のセルにT検定式を書くつもりです。 つまり、
そして、この式はあなたに直接p値を与えるでしょう。<7900><5957>ExcelツールでP値を求めるPak<8370><5732>Taked Pakは、様々な統計的測定値を自動的に計算できるパックなので、簡単で非常に便利です。 取付けることもまた容易です。
ステップ1:設定に移動します。 左隅の下部に「アドイン」ボタンがあり、それをクリックします。 新しいウィンドウが表示され、「Analysis Tool Pak」オプションを見つけてクリックし、ウィンドウの下部にある[go]ボタンをクリックします。
ステップ2:右の列のOKボタンの横にある目盛り記号をクリックして、アドインを有効にします。
ステップ3:適切に有効にすると、ワークシートの上部メニューの右側に”データ分析”ボタンが表示されます。
ステップ4:”データ分析”ボタンをクリックし、”T-Test:Paired Two Sample for Means”オプションを選択します。 その後、[OK]をクリックします。 新しいウィンドウが表示されます。
ステップ5:ウィンドウの最初の行の入力を要求します。 「可変1範囲」ボックスにC4:C13と入力します。 「可変2範囲」ボックスにD4:D13と入力します。 アルファボックスはデフォルト値のままにしておきます。
ステップ6:ウィンドウの2番目の行で、結果を監視する場所を選択できます。 これは、新しいワークシートまたは任意の空白のセルにすることができます。 セルの結果が必要な場合は、列と行をロックしてください。 その後、OKボタンをクリックします。
: 列と行をロックするには、文字と数字の前にドル記号を使用します。 たとえば、A2セルをロックする場合は、$A$2と入力します。ステップ7:Excelは、平均、分散、観測値、ピアソン相関、仮説平均差、t統計、p値などを計算します。最後の言葉
P値は、多くの異なる状況で計算し、適応するのは簡単です。 それはあなたがそれに多くの時間や労力を費やすことなく、必要な情報を取得するのに役立ちます。 適切なツールと数式が付属しているMicrosoft Excelのような統計分析プログラムを使用すると、計算がさらに簡単になります。 のテンプレート集をチェックして、あなたの仕事を楽にするための統計テンプレートをダウンロードしてみましょう!
:
- どのようにExcelで信頼区間を計算するには?
- エクセルはデータを分析できますか?