Miten lasketaan p-arvo Excelissä?

Sisältö

1. 1. Mikä On P-Arvo?
   2. Mihin P-Arvoa Tarvitaan?
   3. Missä Käytetään P-Arvoa Tosielämässä?
      • markkinointi
      • todennäköisyys
   4. Miten lasketaan p-arvo Excelissä?
   5. loppusanat

mikä on P-arvo?

P-arvo on tilastollinen termi, jonka avulla voidaan määrittää otosvaihtelun todennäköisyys, jos käyttämäsi hypoteesi on tosi. Se vain kertoo, millä todennäköisyydellä saamme nämä tulokset, jos nollahypoteesimme on tosi.

• nollahypoteesi on hypoteesi, jonka mukaan saamamme tulokset johtuvat puhtaasta tuurista.
• vaihtoehtoinen hypoteesi väittää, että saamamme tulokset eivät ole tuuria, mutta on ulkopuolisia tekijöitä, jotka vaikuttavat tuloksiimme.

se on erittäin tärkeä ja yleisesti käytetty tilastollinen termi, ja se voidaan helposti laskea tietojen analysointiohjelmissa, kuten Microsoft Excelissä. Tässä artikkelissa opit, miten käytämme sitä, missä käytämme sitä ja miten voimme laskea sen Excelissä eri tavoin.

aloitetaan!

Mihin P-Arvoa Tarvitaan?

suurten populaatioiden tutkimusta tehdessä on laskettava tilastot jokaisesta yksilöstä. Mutta edes tällaisessa tapauksessa, et voi olla varma, jos jotain on tapahtunut, koska sattumaa tai yksinkertaisesti onnea, koska se on mahdotonta tarkkailla kaikkea. Tässä tulevat tilastot.

tilastolliset laskelmat eivät voi antaa absoluuttista totuutta, mutta ne auttavat sinua saamaan hyvän käsityksen tutkimuksistasi.

P-arvo mahdollistaa hypoteesin testaamisen kohteessamme. Voimme verrata matemaattisia tuloksia näihin hypoteeseihin ja harkita uudelleen polkumme kuluttamatta paljon aikaa tutkimukseen.

Missä Käytetään P-Arvoa Tosielämässä?

käytämme todennäköisyysarvoa, jossa yritämme testata hypoteesia. Kyse voi olla tutkimuksesta tai yksinkertaisesta vedosta, jonka teimme ystävämme kanssa.

sitä on helpompi ymmärtää esimerkkien avulla.

markkinointi:

sanotaan, että työskentelet markkinointialalla ja tuore projektisi on viljamainonta.

you have got produced a video for social media and you have got the information for rather users skipped it or watched it for long time.

esimerkkinä videon yhteinen katseluaika on 20 sekuntia. Keskiarvo on 20 sekuntia. Päätit editoida videon iloisemmalla musiikilla.

nyt mistä tunnistat, toimiko se? Tässä vaiheessa käytämme merkitsevyystilastoja.

laadi ensin nollahypoteesi:

nollahypoteesi väittää, että sijoituksen ja saamasi tuloksen välillä ei ole korrelaatiota. Se ei vaikuta tuloksiin.

tässä esimerkissä nollahypoteesi on seuraava: ”kelloaikaan sovellettavien muutosten välillä ei ole mitään yhteyttä.”

sitten vaihtoehtohypoteesi:

vaihtoehtohypoteesi viittaa siihen, että todellisuudessa musiikin vaihtaminen toimi ja nyt ihmiset katsovat mainosta yli 20 sekunnin ajan. Matemaattisesti vaihtoehtoinen hypoteesi sanoo:

” keskiarvo on nyt yli 20 sekuntia.”

laske Merkitsevyystaso:

nyt on asetettava rajakynnys laskemiseksi, onnistuuko vai ei. Tätä kutsutaan merkitsevyystaso on lisäksi kutsutaan alfa-arvo. Se voi olla mikä tahansa prosenttiosuus haluat, se on täysin sinun.

, mutta tässä esimerkissä se on 0,05.

nyt varmuuden laskemiseksi meillä pitäisi aina olla kaikki kelloajan tiedot. Mutta mitä aikaa ja lähteitä, sinun pitäisi ottaa näyte väestöstä:

1. otit 100 ihmisen näytteen.
2. näillä sadalla ihmisellä on 25 sekuntia aikaa katsoa mainosta.
3. se tarkoittaa, että otoksen keskiarvo on 25.

tämä on hyvin yksinkertainen versio laskutoimituksesta. Mutta otoksen keskihajonta lasketaan yleensä tässä asteikossa, jos ei tiedä koko populaation keskihajontaa.

voit käyttää otokselle laskemiasi arvoja, koska ne ovat lähellä populaatioarvoja. Otoksen keskiarvo on lähellä populaation keskiarvoa.

lasketaan p-arvo:

p-arvo näyttää, voimmeko hylätä nollahypoteesin vai emme. Todennäköisyys, että otoksen keskiarvo on suurempi tai yhtä suuri kuin 25 minuuttia, kun otetaan huomioon nollahypoteesi, on tosi.

on kaksi tilannetta, jotka voivat tapahtua.

1. jos p-arvo on pienempi kuin alfa, voidaan nollahypoteesi hylätä. Sinulla on tilastollinen todiste siitä, että vaihtoehtoinen hypoteesi on totta.
2. mutta jos p-arvo on suurempi tai yhtä suuri kuin alfa, nollahypoteesia ei voi hylätä. Se ei tarkoita, että nollahypoteesi on varmasti totta, mutta sitä ei myöskään voida välttää.

todennäköisyys

työstetään toista esimerkkiä.

ystäväsi ja sinä heititte kolikon ilmaan: jos se on klaava, menetät 5 dollaria ja jos se tulee Kruuna, saat 5 dollaria.

• ystäväsi heittää kolikon kerran: se tulee klaavina. Ei se mitään, on 50 prosentin mahdollisuus, että se tulee klaavina. Oletat, että todennäköisyys on 0,5, koska uskot sen olevan reilu kolikko. Tämä on nollahypoteesisi.

• toinen: se on Hänninen. Menetit toiset 5 dollaria, mutta se on OK, koska on vielä hyvä mahdollisuus Kaksi klaavaa peräkkäin. P-arvo on 0,25 ja se on edelleen käypä suhde.
• Kolmas: se on taas hännillä. Kärppien mahdollisuus kolmesti peräkkäin on 0,12. Se ei ole alhainen, joten ei ole tarpeeksi todisteita siitä, että nollahypoteesi ei ole oikea. Mutta alat ajatella, että vaihtoehtoinen hypoteesi voisi olla oikea.
• neljäs: se kääntyy taas hännäksi näet, kuinka mahdollisuudet alkavat olla todella pienet. Se voi olla ihmeellinen sattuma, mutta on vielä 0,6 mahdollisuus ja ei ole vielä tarpeeksi todisteita tukemaan vaihtoehtoista hypoteesi, joka sanoo kolikon on hankala. Odota viidettä volttia.
• viides: se on Hänninen. Mahdollisuus kolikon osoittautuu klaava viisi kertaa peräkkäin on 0,3, joka on hyvin alhainen. Tämä on kohta voit hylätä nollahypoteesin, koska ei ole tarpeeksi todisteita tukemaan sitä enää.

pyydät ystävääsi katsomaan kolikkoa ja kun pidät sitä, huomaat, että siinä on kaksi klaavaa ja se on hankala kolikko.

mikä sai meidät menettämään uskomme nollahypoteesiimme?

reilussa kolikoiden heittelyssä todennäköisyys saada kruuna tai klaava on 50%. Tämä on tilanne, jossa uskomme kolikon olevan oikeudenmukainen, mutta p-arvon laskiessa luottamuksemme siihen hypoteesiin heikkeni myös.

satunnaishäntää ei juuri ole, kun p-arvo laskee alle 0,05: n. Kun siis käytät tätä tilastollista termiä esimerkiksi syöpätutkimuksiin tai ilmastonmuutoksen vaikutuksiin, sen merkitys kasvaa.

 Huom: ei ole mitään erityistä syytä käyttää 0,05 p-arvoa oletuslaskennassa. Kaavan luoja päätti, että se on hyvä luku laskemiseen ja oletuslaskelmat pitävät siitä kiinni. 0,05 tarkoittaa 5: tä prosenttia 100 yksilön populaatiosta, joka kuuluu normaaliin käyrään. Tämä on yksi syy siihen, että sitä käytetään yleisesti. Jos haluat muuttaa sitä laskettaessa sitä itse, voit.

Miten lasketaan p-arvo Excelissä?

p-arvon voi laskea Microsoft Excelissä useammalla kuin yhdellä tavalla. Voit kirjoittaa kaavoja tai voit käyttää analysointityökalua. Tämä artikkeli sisältää, miten se tehdään molemmilla tavoilla.

käytetään klassisia Excel-kaavoja:

aloitetaan klassisella Excel-kaavalla. On olemassa kaksi tapaa tehdä tämä TDIST kaava ja t-testi kaava.

1, 1) TDIST Formula_838>

ensinnäkin tarvitaan tietojoukko p-arvon laskemiseksi.

• sanotaan, että olet opettaja ja haluat vertailla, mitä oppilaasi saivat viime tentissä ja mitä odotit heidän pisteidensä perustuvan heidän aiempiin kokeisiinsa.
• sinulla on tulokset 25, 46, 34, 27, 35, 43, 40, 44, 21 ja 39 viimeisimpään kokeeseesi.
• nyt laskemiseen tarvitset toisen hännän, tätä tulosta odotit aiempien testien perusteella: 23, 44, 32, 20, 46, 37, 35, 42, 33, ja 35

jotta Excelissä voisi käyttää p-arvon kaavaa, kannattaa laskea etukäteen muutama asia:

Pearsonin kerroin (r): Se on tilastotermi, joka mittaa kahden tiedon välistä lineaarista korrelaatiota. P-arvon laskemiseksi ei tarvitse tietää sen matemaattista puolta. Näet sen yksinkertaisen kaavan seuraavissa kappaleissa.

populaatio (n): n on tietokokonaisuutenne henkilöiden kokonaismäärä.

t tilastot: se on tietojen estimoidun arvon poikkeaman suhde oletetusta arvosta keskivirheeseen.

vapausaste: tietoaineistossa olevien henkilöiden lukumäärä miinus kaksi.

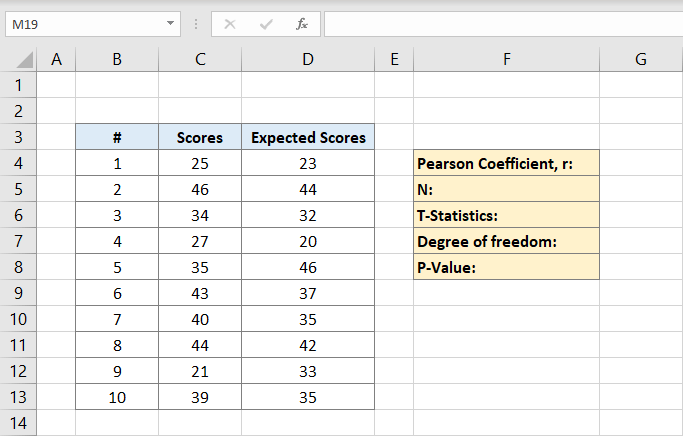
Pearsonin kerroin kirjoitetaan tässä esimerkissä F4: lle. Kun olet napsauttanut sitä, kirjoitat kaavan:

C sarakkeet ovat pistemäärille ja D sarakkeet ovat odotetuille tuloksille. Pearsonin kerroin on tässä esimerkissä 0,691473.

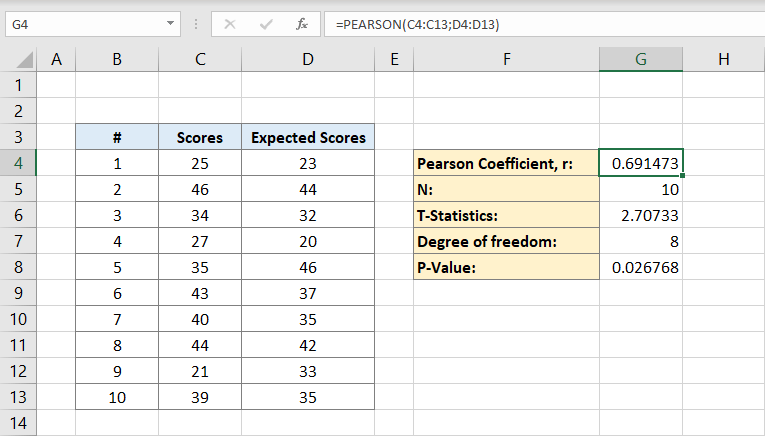
Seuraava, kirjoitat yksilöiden määrä tietoaineistossa. Jos tiedät varmasti, kuinka monta henkilöä sinulla on voit kirjoittaa sen manuaalisesti, mutta jos et voi käyttää kaavaa:

miksi kaavassa on vain C-sarake?

se johtuu siitä, että tarvitsemme vain yhden aineiston henkilöitä laskemaan, joten yksi sarake riittää. Solu G5 sisältää nyt numeron 10. Tässä on väestömme.

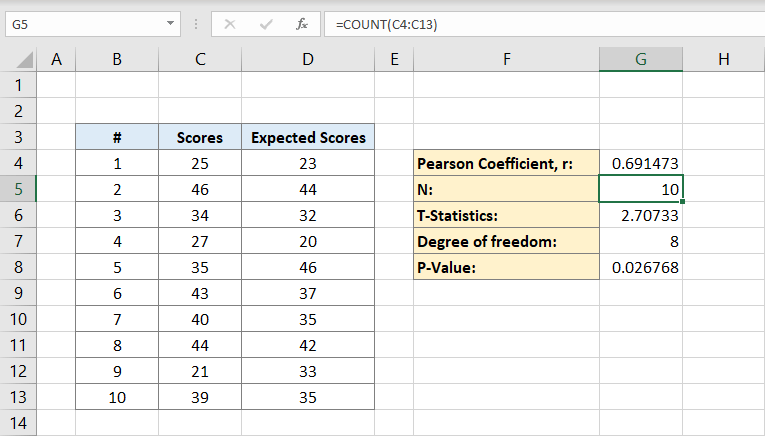
nyt kun sinulla on sekä Pearson kerroin Ja väestö voit laskea t tilastot. T-tilastojen matemaattinen kaava on Pearsonin kerroin (r) kertaa merkin neliöjuuri populaatiosta (n) miinus 2 jaettuna neliöjuurella 1 miinus Pearsonin kerroin potenssiin:

solu G6 sisältää tuloksen 2,70733. Tämä on tilastomme.

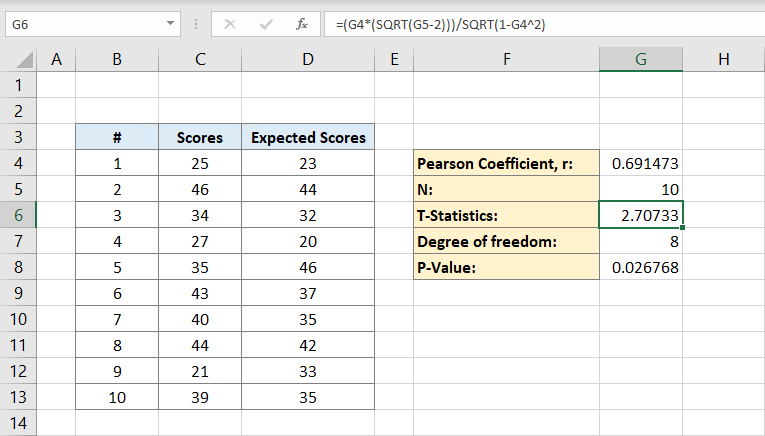
sen jälkeen lasketaan vapausaste. Kirjoitat:

soluun G7. Tämä on vapauden aste. Kello 8.

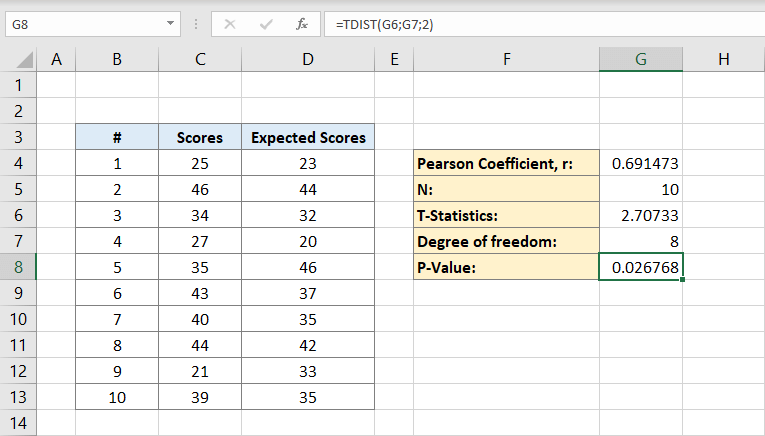
nyt sinulla on kaikki mitä tarvitset P-arvon laskemiseen. Solu G8 sisältää sen kaavan. Eli:

tai

tulos on 0,026768. Tämä on tietoaineiston p-arvo.

1.2. T-testin kaava

toinen tapa määrittää p-arvo Excel-kaavoilla on T-testin kaava. Se on hieman samanlainen kuin edellinen esimerkki, mutta lyhyempi.

• sanotaan, että tietojoukko on sama, sinulla on tulokset 25, 46, 34, 27, 35,43, 40, 44, 21, 39 viimeisimpään kokeeseesi.
• odotetut tulokset ovat 23, 44, 32, 20, 46, 37, 35, 42, 33, 35.
• lisätään kolmas sarake odotetun ja toteutuneen pistemäärän erolle. Erotussarakkeessa 2, 2, 2, 7, 11, 6, 5, 2, 12, 4 kirjoitetaan E4: stä E13: een.

nyt Tyyppi T-testi soluun E8. Kirjoitat t-testin kaavan viereiseen tyhjään soluun. Se on:

ja tämä kaava antaa sinulle p-arvo suoraan.

Määritä p-arvo Excel – työkalulla Pak

otti Pak on pakkaus, jonka avulla voit laskea erilaisia tilastollisia mittauksia automaattisesti, joten se on helppo ja erittäin kätevä. Se on myös helppo asentaa.

Vaihe 1: Siirry asetuksiin. On” Add-ins ” – painiketta alareunassa vasemmassa yläkulmassa, klikkaa sitä. Uusi ikkuna ilmestyy, löytää ”analyysityökalu Pak” vaihtoehto, klikkaa sitä, ja napsauta go-painiketta alareunassa ikkunan.

Vaihe 2: Aktivoi lisäosa klikkaamalla sen vieressä olevaa rasti-symbolia ja oikeassa sarakkeessa olevan OK-painikkeen jälkeen.

Vaihe 3: Jos onnistuit aktivoimaan sen oikein, ”Data analysis” – painike ilmestyy laskentataulukon ylävalikkoon oikealle puolelle.

Vaihe 4: Napsauta ”Data analysis”-painiketta ja valitse ”t-Test: pariksi kaksi näytettä välineille” – vaihtoehto. Napsauta OK sen jälkeen. Uusi ikkuna ilmestyy.

Vaihe 5: se kysyy syötteitä ikkunan ensimmäisellä rivillä. Tyyppi C4: C13″ muuttuja 1 Alue ” – ruutuun. Kirjoitat D4: D13 ”muuttuja 2 alue” ruutuun. Jätä alfa-ruutuun sen oletusarvo.

Vaihe 6: ikkunan toiselta riviltä voit valita, missä voit seurata tuloksiasi. Se voi olla uusi laskentataulukko tai tyhjiä soluja. Jos haluat tuloksen solussa varmista, että lukitset sarakkeen ja rivin. Napsauta OK-painiketta sen jälkeen.

 kärki: Käytä dollar-merkkiä kirjaimen ja numeron edessä lukitaksesi sarakkeen ja rivin. Jos esimerkiksi haluat lukita A2-solun, Kirjoita $a$2.

Vaihe 7: Excel laskee keskiarvon, varianssin, havainnot, Pearsonin korrelaation, hypoteettisen keskiarvoeron, t-tilastoinnin, p-arvon ja paljon muuta.

loppusanat

P-arvo on helppo laskea ja mukauttaa monissa eri tilanteissa. Se auttaa sinua saamaan tarvitsemasi tiedot kuluttamatta paljon aikaa tai vaivaa siihen. On vielä helpompi laskea, kun käytät Microsoft Excelin kaltaisia tilastoanalyysiohjelmia, joissa on oikeat työkalut ja kaavat. Katsotaanpa tarkistaa Someka malleja kokoelma ja ladata tilastollisia malleja tehdä työsi helpompaa!

vastaavat lukemat:

• miten luottamusväli lasketaan Excelissä?
• Voiko Excel Analysoida Tietoja?