keskiarvon keskivirhe tai yksinkertaisesti keskivirhe kertoo, kuinka erilainen perusjoukon keskiarvo todennäköisesti on otoksen keskiarvosta. Se kertoo, kuinka paljon otoksen keskiarvo vaihtelisi, jos toistaisi tutkimuksen, jossa käytettäisiin uusia näytteitä yhden populaation sisältä.
keskiarvon keskivirhe (SE tai SEM) on yleisimmin raportoitu keskivirhetyyppi. Keskivirhe löytyy kuitenkin myös muista tilastoista, kuten mediaaneista tai mittasuhteista. Keskivirhe on yleinen otantavirheen mitta-populaatioparametrin ja otostilaston ero.
miksi keskivirheillä on merkitystä
tilastoissa otosten tietoja käytetään suurempien populaatioiden ymmärtämiseen. Keskivirheellä on merkitystä, koska sen avulla voit arvioida, kuinka hyvin otosaineistosi edustaa koko väestöä.
todennäköisyysotannalla, jossa otoksen elementit valitaan satunnaisesti, voidaan kerätä aineistoa, joka todennäköisesti edustaa populaatiota. Todennäköisyysnäytteistä huolimatta osa otantavirheestä jää kuitenkin jäljelle. Tämä johtuu siitä, että otos ei koskaan täysin vastaa populaatiota, josta se tulee, mitattuna toimenpiteillä, kuten keinoilla ja keskihajonnoilla.
laskemalla keskivirheen voit arvioida, kuinka edustava otoksesi on väestöstäsi, ja tehdä päteviä johtopäätöksiä.
suuri keskivirhe osoittaa, että otoksen keskiarvot ovat laajalti jakautuneet populaation keskiarvon ympärille—otoksesi ei välttämättä edusta väestöäsi tarkasti. Alhainen keskivirhe osoittaa, että otoksen keskiarvot ovat tiiviisti jakautuneet populaation keskiarvon ympärille-otoksesi edustaa väestöäsi.
keskivirhettä voi pienentää suurentamalla otoskokoa. Käyttämällä suuri, satunnainen otos on paras tapa minimoida näytteenottoharha.
keskivirhe vs keskihajonta
keskivirhe ja keskihajonta ovat molemmat vaihtelun mittareita:
- keskihajonta kuvaa vaihtelua yksittäisen näytteen sisällä.
- keskivirhe Arvioi populaation useiden otosten vaihtelua.


keskihajonta on kuvaava tilasto, joka voidaan laskea otosaineistosta. Sen sijaan keskivirhe on päätelty tilasto, joka voidaan arvioida vain (ellei reaaliväestön parametria tunneta).
matematiikan pisteiden keskihajonta on 180. Luku kertoo keskimäärin, kuinka paljon kukin pistemäärä poikkeaa otoksen keskiarvosta 550.
matematiikkapisteiden keskivirhe taas kertoo, kuinka paljon otoskeskiarvo 550 eroaa muista otoskeskiarvoista samansuuruisissa otoksissa kaikkien alueen kokeiden ottajien populaatiossa.
keskivirhe formula_9629>
keskiarvon keskivirhe lasketaan keskihajonnan ja otoskoon avulla.
kaavasta näkee, että otoskoko on kääntäen verrannollinen keskivirheeseen. Tämä tarkoittaa, että mitä suurempi otos, sitä pienempi keskivirhe, koska otostilasto on lähempänä populaatioparametria.
käytetään erilaisia kaavoja riippuen siitä, onko populaation keskihajonta tiedossa. Nämä kaavat toimivat näytteille, joissa on yli 20 alkuainetta (n > 20).
kun populaatioparametrit ovat tiedossa
kun populaation keskihajonta on tiedossa, voidaan sen avulla laskea tarkasti keskivirhe alla olevassa kaavassa.
| Formula_3917 > | selitys |
|---|---|
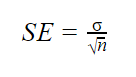 |
|
kun populaatioparametrit eivät ole tiedossa
kun populaation keskihajonta on tuntematon, voit käyttää alla olevaa kaavaa vain keskivirheen estimointiin. Tässä kaavassa otoksen keskihajonta on populaation keskihajonnan piste-estimaatti.
| Formula_3917 > | selitys |
|---|---|
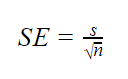 |
|
etsi ensin otoskokosi neliöjuuri (n).
| Formula_3917> | laskutoimitus |
|---|---|
| √ | n = 200
√n = √200 = 14.1 |
Jaa seuraavaksi näytteen keskihajonta vaiheesta yksi löytämälläsi luvulla.
| Formula_3917> | laskutoimitus |
|---|---|
| se = s ¾ √ n | s = 180
√n = 14, 1 s = 180 ÷ 14.1 = 12.8 |
matematiikan SAT-pisteiden keskivirhe on 12,8.
miten keskivirhe ilmoitetaan?
keskivirhe voidaan ilmoittaa keskiarvon rinnalla tai luottamusvälillä keskiarvon ympärillä olevan epävarmuuden ilmoittamiseksi.
keskivirhe ilmoitetaan parhaiten luottamusvälillä, koska lukijoiden ei tarvitse tehdä mitään ylimääräistä matematiikkaa keksiäkseen mielekkään intervallin.
luottamusväli on arvojen vaihteluväli, jossa tuntemattoman populaatioparametrin odotetaan olevan suurimman osan ajasta, jos tutkimus toistetaan uusilla satunnaisnäytteillä.
95 prosentin luotettavuustasolla 95 prosentin kaikista otoksen keskiarvoista oletetaan olevan ± 1, 96 otoksen keskiarvon keskivirheen luottamusvälin sisällä.
satunnaisotannan perusteella myös todellisen populaatioparametrin arvioidaan sijoittuvan tälle vaihteluvälille 95 prosentin varmuudella.
tavanomaisesti jakautuvan ominaisuuden, kuten SAT-pisteiden, osalta 95% kaikista otoksen keskiarvoista sijoittuu noin 4 otoksen keskiarvon keskivirheen sisään.
| Luottamusvälikaava | |
|---|---|
|
CI = x ± (1, 96 × SE) x = näytteen keskiarvo = 550 |
|
| alaraja | yläraja |
|
x − (1.96 × SE) 550 − (1.96 × 12.8) = 525 |
x + (1,96 × SE) 550 + (1.96 × 12.8) = 575 |
satunnaisotannalla 95%: n luottamusväli kertoo, että on 0,95 todennäköisyys, että populaation keskiarvo math SAT-pisteet ovat välillä 525 ja 575.
muut keskivirheet
keskiarvon keskivirheen (ja muiden tilastojen) lisäksi on kaksi muuta keskivirhettä, joihin saatat törmätä: estimaatin keskivirhe ja mittauksen keskivirhe.
estimaatin keskivirhe liittyy regressioanalyysiin. Tämä kuvastaa estimoidun regressiolinjan ympärillä olevaa vaihtelua ja regressiomallin tarkkuutta. Estimaatin keskivirheen avulla voidaan muodostaa luottamusväli todelliselle regressiokertoimelle.
mittauksen keskivirhe kertoo mittauksen luotettavuudesta. Se osoittaa, kuinka vaihteleva testin mittausvirhe on, ja se ilmoitetaan usein standardoiduissa testeissä. Mittauksen keskivirheen avulla voidaan luoda luottamusväli alkuaineen tai yksilön todelliselle pisteelle.
Usein kysyttyä keskivirheestä
keskiarvon keskivirhe tai yksinkertaisesti keskivirhe kertoo, kuinka erilainen perusjoukon keskiarvo todennäköisesti on otoksen keskiarvosta. Se kertoo, kuinka paljon otoksen keskiarvo vaihtelisi, jos toistaisi tutkimuksen, jossa käytettäisiin uusia näytteitä yhden populaation sisältä.
keskivirhe ja keskihajonta ovat molemmat vaihtelun mittareita. Keskihajonta heijastaa vaihtelua otoksen sisällä, kun taas keskivirhe arvioi vaihtelua populaation otosten välillä.
kuvailevien ja päättelevien tilastojen avulla voidaan populaatiosta tehdä kahdenlaisia estimaatteja: piste-estimaatteja ja intervalliestimaatteja.
- piste-estimaatti on parametrin yksittäinen arvo-estimaatti. Otoskeskiarvo on esimerkiksi populaation keskiarvon piste-estimaatti.
- intervalliarvio antaa vaihteluvälin, johon parametrin oletetaan sijoittuvan. Luottamusväli on yleisin intervalli-estimaatin tyyppi.
molemmat estimaatit ovat tärkeitä, jotta saadaan selkeä käsitys siitä, missä jokin parametri todennäköisesti sijaitsee.
