standardfelet för medelvärdet, eller helt enkelt standardfel, indikerar hur olika populationsmedlet sannolikt kommer att vara från ett provmedelvärde. Det berättar hur mycket provmedlet skulle variera om du skulle upprepa en studie med nya prover från en enda population.
standardfelet för medelvärdet (SE eller SEM) är den vanligaste rapporterade typen av standardfel. Men du kan också hitta standardfelet för annan statistik, som medianer eller proportioner. Standardfelet är ett vanligt mått på provtagningsfel-skillnaden mellan en populationsparameter och en provstatistik.
varför standardfel är viktigt
i statistik används data från prover för att förstå större populationer. Standardfel är viktigt eftersom det hjälper dig att uppskatta hur bra dina provdata representerar hela befolkningen.
med sannolikhetsprovtagning, där element i ett prov väljs slumpmässigt, kan du samla in data som sannolikt är representativa för befolkningen. Men även med sannolikhetsprover kommer vissa provtagningsfel att förbli. Det beror på att ett prov aldrig perfekt matchar befolkningen det kommer från när det gäller åtgärder som medel och standardavvikelser.
genom att beräkna standardfel kan du uppskatta hur representativt ditt prov är av din befolkning och göra giltiga slutsatser.
ett högt standardfel visar att provmedlen är brett spridda runt populationsmedlet—ditt prov kanske inte representerar din population nära. Ett lågt standardfel visar att provmedlen är nära fördelade runt befolkningsmedlet—ditt prov är representativt för din befolkning.
du kan minska standardfel genom att öka provstorleken. Att använda ett stort slumpmässigt prov är det bästa sättet att minimera provtagningsförspänning.
standardfel vs standardavvikelse
standardfel och standardavvikelse är båda mått på variabilitet:
- standardavvikelsen beskriver variabilitet inom ett enda prov.
- standardfelet uppskattar variationen mellan flera prover av en population.


standardavvikelsen är en beskrivande statistik som kan beräknas från provdata. Däremot är standardfelet en inferentiell statistik som endast kan uppskattas (såvida inte den verkliga populationsparametern är känd).
standardavvikelsen för matematiska poäng är 180. Detta antal återspeglar i genomsnitt hur mycket varje poäng skiljer sig från provets genomsnittliga poäng på 550.
standardfelet för matematiska poäng, å andra sidan, berättar hur mycket provmedelvärdet på 550 skiljer sig från andra provmedelvärden, i prover av samma storlek, i befolkningen i alla testtagare i regionen.
standardfelformel
standardfelet för medelvärdet beräknas med standardavvikelsen och provstorleken.
från formeln ser du att provstorleken är omvänt proportionell mot standardfelet. Detta innebär att ju större provet är, desto mindre är standardfelet, eftersom provstatistiken kommer att närma sig populationsparametern.
olika formler används beroende på om populationens standardavvikelse är känd. Dessa formler fungerar för prover med mer än 20 Element (n > 20).
när populationsparametrar är kända
när populationsstandardavvikelsen är känd kan du använda den i nedanstående formel för att beräkna standardfel exakt.
| formel | förklaring |
|---|---|
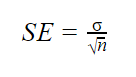 |
|
när populationsparametrarna är okända
när populationsstandardavvikelsen är okänd kan du använda nedanstående formel för att bara uppskatta standardfel. Denna formel tar provstandardavvikelsen som en punktuppskattning för populationens standardavvikelse.
| formel | förklaring |
|---|---|
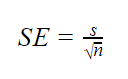 |
|
hitta först kvadratroten av din provstorlek (n).
| formel | beräkning |
|---|---|
| √n | n = 200
= √200 = 14.1 |
därefter dela provstandardavvikelsen med det nummer du hittade i steg ett.
| formel | beräkning |
|---|---|
| se = s 0 | s = 180
24,1 84,1= 180 ÷ 14.1 = 12.8 |
standardfelet för math SAT-poäng är 12,8.
hur ska du rapportera standardfelet?
du kan rapportera standardfelet tillsammans med medelvärdet eller i ett konfidensintervall för att kommunicera osäkerheten kring medelvärdet.
det bästa sättet att rapportera standardfelet är i ett konfidensintervall eftersom läsarna inte behöver göra någon ytterligare matematik för att komma med ett meningsfullt intervall.
ett konfidensintervall är ett värdeområde där en okänd populationsparameter förväntas ligga för det mesta, om du skulle upprepa din studie med nya slumpmässiga prover.
med en konfidensnivå på 95% förväntas 95% av alla provmedel ligga inom ett konfidensintervall på 1,96 standardfel i provmedelvärdet.
baserat på slumpmässigt urval beräknas den verkliga populationsparametern också ligga inom detta intervall med 95% förtroende.
för en normalt distribuerad egenskap, som SAT-poäng, faller 95% av alla provmedel inom ungefär 4 standardfel i provmedlet.
| formel för konfidensintervall | |
|---|---|
|
CI = x (1,96 (155)> X = medelvärde för provet = 550 |
|
| nedre gräns | övre gräns |
|
x − (1.96 oz. se) 550 − (1.96 × 12.8) = 525 |
x + (1,96 oc) 550 + (1.96 × 12.8) = 575 |
med slumpmässigt urval berättar en 95% CI att det finns en 0,95 sannolikhet att populationens genomsnittliga math SAT-poäng är mellan 525 och 575.
andra standardfel
bortsett från standardfelet för medelvärdet (och annan statistik) finns det två andra standardfel som du kan stöta på: standardfelet för uppskattningen och standardfelet för mätning.
standardfelet i uppskattningen är relaterat till regressionsanalys. Detta återspeglar variationen kring den uppskattade regressionslinjen och regressionsmodellens noggrannhet. Med hjälp av standardfelet i uppskattningen kan du konstruera ett konfidensintervall för den sanna regressionskoefficienten.
standardfelet för mätning handlar om tillförlitligheten hos en åtgärd. Det indikerar hur variabelt mätfelet för ett test är, och det rapporteras ofta i standardiserad testning. Standardfelet för mätning kan användas för att skapa ett konfidensintervall för den verkliga poängen för ett element eller en individ.
Vanliga frågor om standardfel
standardfelet för medelvärdet, eller helt enkelt standardfelet, indikerar hur olika populationsmedlet sannolikt kommer att vara från ett provmedelvärde. Det berättar hur mycket provmedlet skulle variera om du skulle upprepa en studie med nya prover från en enda population.
standardfel och standardavvikelse är båda mått på variabilitet. Standardavvikelsen återspeglar variabilitet inom ett prov, medan standardfelet uppskattar variationen mellan prover av en population.
med hjälp av beskrivande och inferentiell statistik kan du göra två typer av uppskattningar om befolkningen: punktuppskattningar och intervalluppskattningar.
- en punktuppskattning är en enda värdeuppskattning av en parameter. Till exempel är ett provmedel en punktuppskattning av ett populationsmedel.
- en intervalluppskattning ger dig ett intervall av värden där parametern förväntas ligga. Ett konfidensintervall är den vanligaste typen av intervalluppskattning.
båda typerna av uppskattningar är viktiga för att samla en klar uppfattning om var en parameter sannolikt kommer att ligga.
