hur man beräknar p-värde i Excel?

Innehåll

1. 1. Vad Är P-Värdet?
   2. Varför Behöver Vi P-Värdet?
   3. Var Använder Vi P-Värdet I Verkligheten?
      • marknadsföring
      • Sannolikhet
   4. hur man beräknar p-värdet i Excel?
   5. sista ord

Vad är P-värdet?

P-värde är en statistisk term som hjälper dig att bestämma, om hypotesen du använder är sant, sannolikheten för provtagningsvariationen. Det berättar helt enkelt vad är oddsen för att få dessa resultat om vår nollhypotes är sant.

• en nollhypotes är en hypotes som hävdar att resultaten vi får orsakas av ren tur.
• en alternativ hypotes hävdar att resultaten vi får inte är tur men det finns yttre element som påverkar våra resultat.

det är en mycket viktig och vanligt förekommande statistisk term och kan enkelt beräknas i dataanalysprogram som Microsoft Excel. I den här artikeln lär du dig hur vi använder den, var använder vi den och hur kan vi beräkna den i Excel på olika sätt.

Låt oss börja!

Varför Behöver Vi P-Värdet?

medan du gör forskning med stora populationer måste du beräkna statistiken för varje individ. Men även i ett sådant fall kan du inte vara säker på om något hände på grund av slump eller helt enkelt tur eftersom det är omöjligt att observera allt. Det är här statistiken kommer in.

statistiska beräkningar kan inte ge dig en absolut sanning men de hjälper dig att få en bra uppfattning om dina undersökningar.

P-värde tillåter oss att testa hypotesen om vårt ämne. Vi kan jämföra de matematiska resultaten med dessa hypoteser och ompröva vår väg utan att spendera mycket tid på forskning.

Var Använder Vi P-Värdet I Verkligheten?

vi använder sannolikhetsvärdet där vi försöker testa en hypotes. Det kan handla om forskning eller en enkel satsning vi gjorde med vår vän.

det är lättare att förstå det med exempel.

marknadsföring:

låt oss säga att du arbetar inom marknadsföringsområdet och ditt senaste projekt handlar om spannmålsreklam.

du har producerat en video för sociala medier och du har fått informationen för snarare användare hoppade över den eller tittade på den länge.

som ett exempel är den vanliga visningstiden för videon 20 sekunder. Medelvärdet är 20 sekunder. Och du fattade beslutet att redigera videon med en bit av mer glädjande Musik.

nu Hur kommer du att känna igen om det fungerade? Vid denna tidpunkt använder vi signifikansstatistik.

först producera en nollhypotes:

en nollhypotes hävdar att det inte finns någon korrelation mellan vad du investerar och de resultat du får. Det påverkar inte resultaten.

under det här exemplet kommer nollhypotesen att vara så här: ”Det finns inget samband mellan de ändringar du tillämpar på visningstiden.”

sedan den alternativa hypotesen:

den alternativa hypotesen antyder att det faktiskt fungerade att ändra musiken och nu tittar folk på reklamen i mer än 20 sekunder. Matematiskt säger den alternativa hypotesen:

” medelvärdet är större än 20 sekunder nu.”

beräkna signifikansnivån:

nu måste vi ställa in en gränströskel för att beräkna om vi lyckas eller inte. Detta kallas en signifikansnivå kallas dessutom alfavärdet. Det kan vara vilken procentandel du vill, det är helt upp till dig.

men under det här exemplet blir det 0,05.

nu för att beräkna med säkerhet bör vi alltid ha alla data om klocktid. Men när det gäller din tid och källor bör du ta ett prov från befolkningen:

1. du tog ett urval av 100 personer.
2. dessa 100 personer har 25 sekunders visningstid för reklamen.
3. det betyder att provmedlet är 25.

detta är en mycket enkel version av beräkningen. Men standardavvikelsen för provet beräknas vanligtvis i denna skala om du inte känner till standardavvikelsen för hela befolkningen.

du kan använda de värden du beräknade för provet eftersom de ligger nära populationsvärdena. Provmedlet ligger nära befolkningens medelvärde.

beräkna P-värdet:

p-värdet visar oss om vi kan avvisa nollhypotesen eller inte. Sannolikheten att provmedlet är större än eller lika med 25 minuter med tanke på nollhypotesen är sant.

det finns två situationer som kan hända.

1. om p-värdet är mindre än alfa kan du avvisa nollhypotesen. Du har statistiska bevis på att den alternativa hypotesen är sant.
2. men om p-värdet är större eller lika med alfa kan du inte avvisa nollhypotesen. Det betyder inte att nollhypotesen verkligen är sant men den kan inte heller undvikas.

Sannolikhet

låt oss arbeta med ett annat exempel.

din vän och du gjorde kasta mynt i luften: om det är svansar du förlorar 5 dollar och om det kommer huvuden du får 5 dollar.

• din vän vänder myntet en gång: det kommer som svansar. Det är okej, det finns en 50% chans att det kommer som svansar. Nu antar du att sannolikheten är 0,5 eftersom du tror att det är ett rättvist mynt. Detta är din nollhypotes.

• andra: det är svansar. Du förlorade ytterligare 5 dollar men det är okej eftersom det fortfarande finns en god chans att två svansar i rad. P-värdet är 0,25 och det är fortfarande ett rättvist förhållande.
• tredje: det är svansar igen. Chansen att svansar tre gånger i rad är 0,12. Det är inte lågt så det finns inte tillräckligt med bevis för att nollhypotesen inte är korrekt. Men du börjar tro att din alternativa hypotes kan vara korrekt.
• fjärde: det blir som svansar igen du kommer att se hur chanserna blir riktigt låga. Det kan vara en mirakulös tillfällighet men det finns fortfarande en 0,6 chans och det finns fortfarande inte tillräckligt med bevis för att stödja den alternativa hypotesen som säger att myntet är knepigt. Och du väntar på den femte luckan.
• femte: det är svansar. Chansen att ett mynt visar sig som svansar fem gånger i rad är 0,3 vilket är mycket lågt. Det här är den punkt Du kan avvisa nollhypotesen för det finns inte tillräckligt med bevis för att stödja det längre.

du ber din vän att se myntet och när du håller det inser du att det har två svansar sida och det är ett knepigt mynt.

Vad fick oss att förlora tron på vår nollhypotes?

i en rättvis omgång vända mynt, är chansen att få en krona eller klave 50%. Det här är en situation där vi tror att myntet är rättvist men eftersom p-värdet sjunker vårt förtroende för den hypotesen försvagades också.

det finns liten chans att ha slumpmässiga svansar när p-värdet sjunker under 0,05. Så när du tillämpar denna statistiska term på frågor som cancerforskningar eller effekter av klimatförändringar får det större betydelse.

 Obs: Det finns ingen särskild anledning att vi använder 0,05 p-värde för standardberäkning. Skaparen av formeln bestämde att det var ett bra tal för beräkning och standardberäkningarna håller fast vid det. 0,05 betyder 5% i 100 individer populationer som faller in i den normala kurvan. Detta är en av anledningarna till att det vanligtvis används. Om du vill ändra det under beräkningen själv kan du.

hur man beräknar p-värdet i Excel?

det finns mer än ett sätt att beräkna p-värdet i Microsoft Excel. Du kan skriva ner formler eller du kan använda Analysis ToolPak. Den här artikeln innehåller hur man gör det båda sätten.

användning av klassiska Excel-formler:

Låt oss börja med den klassiska Excel-formeln. Det finns två sätt att göra denna tdistformel och t-testformel.

1.1) Tdist-formel

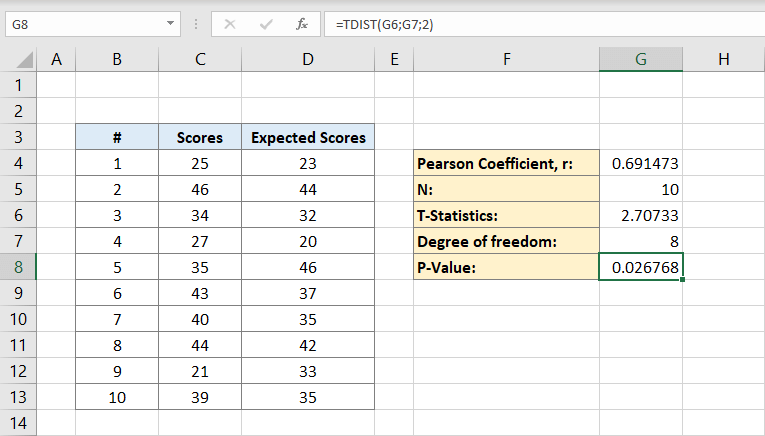
först och främst behöver du en datamängd för att beräkna ett p-värde.

• låt oss säga att du är lärare och du vill jämföra vad dina elever gjorde i din senaste tentamen och vad du förväntade dig att deras poäng skulle baseras på deras tidigare tentor.
• du har resultaten 25, 46, 34, 27, 35, 43, 40, 44, 21 och 39 för din senaste tentamen.
• nu för beräkning behöver du en annan svans, det här är poängen du förväntade dig baserat på tidigare test: 23, 44, 32, 20, 46, 37, 35, 42, 33, och 35

för att kunna använda p-värdeformeln på Excel bör du beräkna några saker i förväg:

Pearson-koefficient (r): Det är en statistisk term som mäter den linjära korrelationen mellan två data. Du behöver inte känna till den matematiska aspekten av den för att beräkna p-värdet. Du kommer att se den enkla formeln för den i nästa stycke.

Population (n): n är det totala antalet individer i din datamängd.

t statistik: Det är förhållandet mellan avvikelsen för data uppskattat värde från dess antagna värde till dess standardfel.

frihetsgrad: det är antalet individer i datamängden minus två.

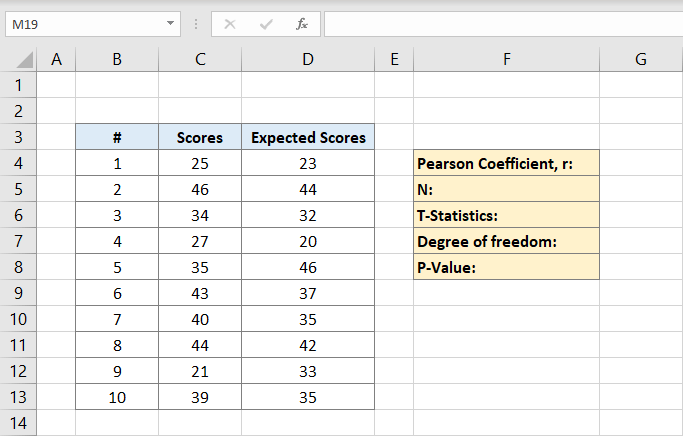
nu kommer Pearson-koefficienten att skrivas på F4 i detta exempel. När du klickar på den skriver du formeln:

C-kolumner är för poängen och D-kolumner är för de förväntade poängen. Pearson-koefficienten är 0,691473 i detta exempel.

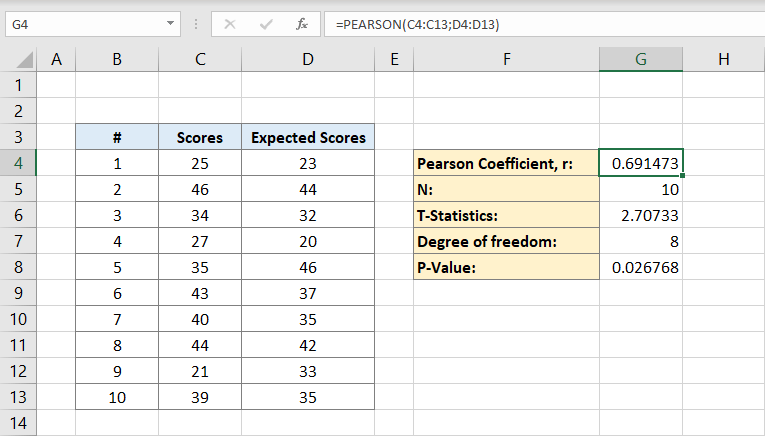
därefter skriver du antalet individer i datamängden. Om du vet säkert hur många individer du har kan du skriva det manuellt men om du inte kan du använda formeln:

varför innehåller formeln endast en C-kolumn?

det beror på att vi bara behöver individerna i en dataset för att beräkna, därför kommer en kolumn att göra. Cellen G5 kommer nu att innehålla numret 10 i den. Detta är vår befolkning.

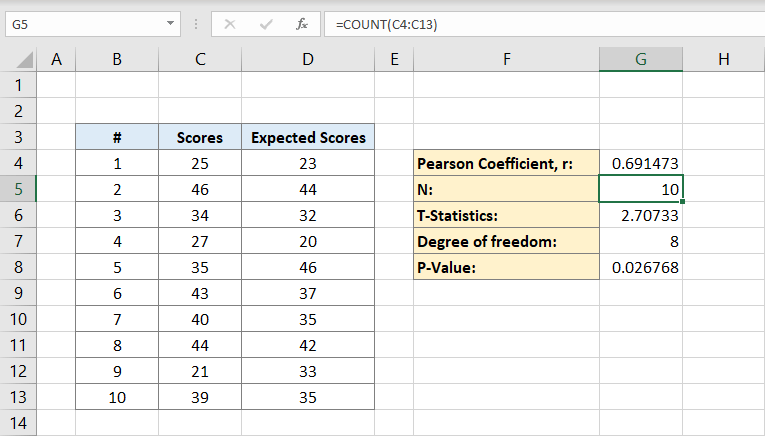
nu när du har både Pearson-koefficienten och befolkningen kan du beräkna t-statistiken. Den matematiska formeln för T statistik är Pearson koefficient (r) gånger tecken kvadratroten av befolkningen (n) minus 2 dividerat med kvadratroten av 1 minus Pearson koefficient kvadrat:

cellen G6 kommer att innehålla resultatet 2,70733. Detta är vår T-statistik.

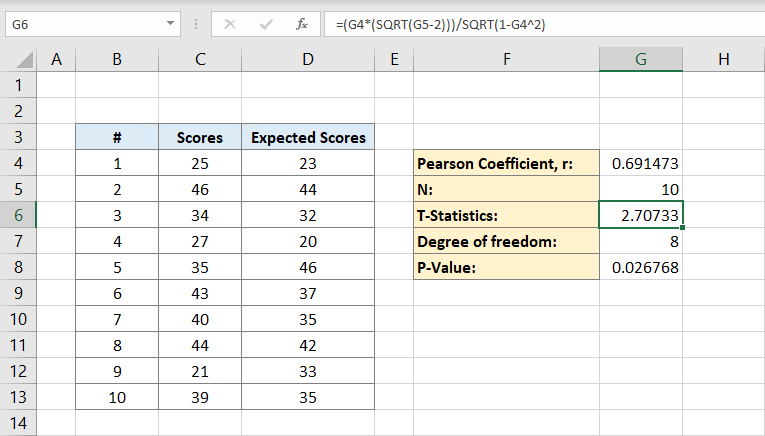
därefter beräknar du graden av frihet. Du skriver:

till cellen G7. Detta är graden av frihet. Det kommer att vara vid 8.

nu har du allt du behöver för att beräkna P-värdet. Cellen G8 kommer att innehålla formeln för den. Det vill säga:

eller

resultatet blir 0,026768. Detta är p-värdet för datamängden.

1.2. T-Testformeln

det andra sättet att bestämma p-värdet med Excel-formler är att använda T-testformeln. Det är lite som föregående exempel men kortare.

• låt oss säga att datamängden är densamma, du har resultaten 25, 46, 34, 27, 35,43, 40, 44, 21, 39 för din senaste examen.
• förväntade resultat är 23, 44, 32, 20, 46, 37, 35, 42, 33, 35.
• du kommer att lägga till en tredje kolumn för skillnaden mellan vad som förväntades och den faktiska poängen. I kolumnen skillnad 2, 2, 2, 7, 11, 6, 5, 2, 12, 4 kommer att skrivas från E4 till E13.

Skriv nu T-Test till cellen E8. Du kommer att skriva t-testformeln till den tomma cellen bredvid den. Det vill säga:

och denna formel ger dig p-värdet direkt.

Bestäm p-värdet med Excel-verktyget Pak

tog Pak är ett paket som låter dig beräkna olika statistiska mätningar automatiskt så det är enkelt och mycket praktiskt. Det är också lätt att installera.

Steg 1: Gå till Inställningar. Det finns en ”Add-ins” – knapp längst ner i vänstra hörnet, Klicka på den. Ett nytt fönster visas, hitta alternativet ”Analysis Tool Pak”, klicka på det och klicka sedan på go-knappen längst ner i fönstret.

steg 2: aktivera tillägget genom att klicka på kryssrutan bredvid den och efter OK-knappen i den högra kolumnen.

steg 3: Om du lyckades aktivera det ordentligt visas en ”dataanalys” – knapp på toppmenyn i ditt kalkylblad till höger.

steg 4: Klicka på knappen ”dataanalys” och välj alternativet ”T-Test: parat två prov för medel”. Klicka på OK efter det. Ett nytt fönster visas.

Steg 5: det kommer att fråga ingångarna i den första raden i fönstret. Skriv C4: C13 till rutan” variabel 1 intervall”. Du skriver D4: D13 till rutan ”variabel 2-intervall”. Lämna alfa-rutan med standardvärdet.

steg 6: i den andra raden i fönstret kan du välja var du vill övervaka dina resultat. Det kan vara ett nytt kalkylblad eller några tomma celler. Om du vill ha resultatet på en cell, se till att du låser kolumnen och raden. Klicka på OK-knappen efter det.

tips: Använd dollartecknet före bokstaven och numret för att låsa kolumnen och raden. Om du till exempel vill låsa A2-cellen skriver du $a$2.

Steg 7: Excel beräknar medelvärdet, variansen, observationerna, Pearson-korrelationen, hypotesen genomsnittlig skillnad, t-statistik, p-värde och mer.

slutord

p-värde är lätt att beräkna och anpassa i många olika situationer. Det hjälper dig att få den information du behöver utan att spendera mycket tid eller ansträngning på den. Det är ännu enklare att beräkna när du använder statistiska analysprogram som Microsoft Excel som kommer med rätt verktyg och formler. Låt oss kolla someka mallar samling och ladda ner statistiska mallar för att göra ditt jobb enklare!

relaterade avläsningar:

• hur man beräknar konfidensintervall i Excel?
• Kan Excel Analysera Data?