o erro padrão da média, ou simplesmente erro padrão, indica quão diferente a média da população provavelmente será de uma média de amostra. Ele informa o quanto a média da amostra variaria se você repetisse um estudo usando novas amostras de uma única população.
o erro padrão da média (se ou SEM) é o tipo de erro padrão mais comumente relatado. Mas você também pode encontrar o erro padrão para outras estatísticas, como medianas ou proporções. O erro padrão é uma medida comum de erro de amostragem – a diferença entre um parâmetro de população e uma estatística de amostra.
por que o erro padrão importa
nas estatísticas, os dados das amostras são usados para entender populações maiores. O erro padrão é importante porque ajuda a estimar o quão bem seus dados de amostra representam toda a população.
com amostragem de probabilidade, onde elementos de uma amostra são selecionados aleatoriamente, você pode coletar dados que provavelmente serão representativos da população. No entanto, mesmo com amostras de probabilidade, algum erro de amostragem permanecerá. Isso porque uma amostra nunca corresponderá perfeitamente à população de onde vem em termos de medidas como meios e desvios padrão.
ao calcular o erro padrão, você pode estimar o quão representativa sua amostra é de sua população e tirar conclusões válidas.
um erro de alto padrão mostra que os meios de amostra estão amplamente espalhados pela média da população—sua amostra pode não representar De Perto sua população. Um erro padrão baixo mostra que os meios de amostra estão intimamente distribuídos em torno da média da população—sua amostra é representativa de sua população.
você pode diminuir o erro padrão aumentando o tamanho da amostra. Usar uma amostra grande e Aleatória é a melhor maneira de minimizar o viés de amostragem.
erro-Padrão vs desvio padrão
erro-Padrão e o desvio padrão são medidas de variabilidade:
- O desvio padrão descreve a variabilidade dentro de uma única amostra.
- o erro padrão estima a variabilidade em várias amostras de uma população.


O desvio padrão é uma estatística descritiva, que pode ser calculado a partir de dados de exemplo. Em contraste, o erro padrão é uma estatística inferencial que só pode ser estimada (a menos que o parâmetro população real seja conhecido).
o desvio padrão das Pontuações matemáticas é 180. Esse número reflete, em média, o quanto cada pontuação difere da pontuação média da amostra de 550.
o erro padrão das Pontuações matemáticas, por outro lado, informa o quanto a pontuação média da amostra de 550 difere de outras pontuações médias da amostra, em amostras de tamanho igual, na população de todos os participantes do teste na região.
o erro Padrão de fórmula
O erro padrão da média é calculado usando o desvio padrão e o tamanho da amostra.
da fórmula, você verá que o tamanho da amostra é inversamente proporcional ao erro padrão. Isso significa que quanto maior a amostra, menor o erro padrão, porque a estatística da amostra estará mais próxima de se aproximar do parâmetro população.
fórmulas diferentes são usadas dependendo se o desvio padrão da população é conhecido. Essas fórmulas funcionam para amostras com mais de 20 elementos (n > 20).
quando os parâmetros populacionais são conhecidos
quando o desvio padrão populacional é conhecido, você pode usá-lo na fórmula abaixo para calcular o erro padrão com precisão.
| Fórmula | Explicação |
|---|---|
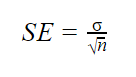 |
|
Quando os parâmetros populacionais são desconhecidas
Quando o desvio padrão da população é desconhecido, você pode utilizar a fórmula abaixo para apenas estimar o erro padrão. Esta fórmula toma o desvio padrão da amostra como uma estimativa pontual para o desvio padrão da população.
| Fórmula | Explicação |
|---|---|
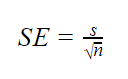 |
|
primeiro, Encontre a raiz quadrada do tamanho da amostra (n).
| Fórmula | Cálculo |
|---|---|
| √n | n = 200
√n = √200 = 14.1 |
em seguida, dividir o desvio padrão da amostra pelo número que você encontrou no passo um.
| Fórmula | Cálculo |
|---|---|
| SE = s ÷ √n | s = 180
√n = 14.1 s ÷ √n = 180 ÷ 14.1 = 12.8 |
O erro padrão da matemática SAT é 12.8.
como você deve relatar o erro padrão?
você pode relatar o erro padrão ao lado da média ou em um intervalo de confiança para comunicar a incerteza em torno da média.
a melhor maneira de relatar o erro padrão é em um intervalo de confiança porque os leitores não terão que fazer nenhuma matemática adicional para chegar a um intervalo significativo.
um intervalo de confiança é um intervalo de valores em que se espera que um parâmetro de população desconhecido fique na maioria das vezes, se você repetir seu estudo com novas amostras aleatórias.
com um nível de confiança de 95%, espera-se que 95% de todas as médias da amostra estejam dentro de um intervalo de confiança de ± 1,96 erros padrão da média da amostra.
com base na amostragem aleatória, estima-se também que o parâmetro da população verdadeira esteja dentro dessa faixa com 95% de confiança.
para uma característica normalmente distribuída, como as pontuações SAT, 95% de todas as médias da amostra estão dentro de cerca de 4 erros padrão da média da amostra.
| intervalo de Confiança de fórmula | |
|---|---|
|
CI = x ± (1.96 × SE) x = média da amostra = 550 |
|
| limite Inferior | limite Superior |
|
x − (1.96 × SE) 550 − (1.96 × 12.8) = 525 |
x + (1.96 × SE) 550 + (1.96 × 12.8) = 575 |
Com amostragem aleatória, um CI de 95% indica que não é um 0.95 probabilidade de que a média da população de matemática do SAT escore está entre 525 e 575.
Outros erros padrão
Além do erro padrão da média (e outras estatísticas), há dois outros erros padrão você poderá encontrar: o erro padrão da estimativa e o erro padrão de medida.
o erro padrão da estimativa está relacionado à análise de regressão. Isso reflete a variabilidade em torno da linha de regressão estimada e a precisão do modelo de regressão. Usando o erro padrão da estimativa, você pode construir um intervalo de confiança para o coeficiente de regressão real.
o erro padrão de medição é sobre a confiabilidade de uma medida. Indica quão variável é o erro de medição de um teste e geralmente é relatado em testes padronizados. O erro padrão de medição pode ser usado para criar um intervalo de confiança para a pontuação verdadeira de um elemento ou de um indivíduo.
Perguntas frequentes sobre erro padrão
o erro padrão da média, ou simplesmente erro padrão, indica quão diferente é provável que a média da população seja de uma média da amostra. Ele informa o quanto a média da amostra variaria se você repetisse um estudo usando novas amostras de uma única população.
erro padrão e desvio padrão são ambas medidas de variabilidade. O desvio padrão reflete a variabilidade dentro de uma amostra, enquanto o erro padrão estima a variabilidade entre as amostras de uma população.
usando estatísticas descritivas e inferenciais, você pode fazer dois tipos de estimativas sobre a população: estimativas pontuais e estimativas de intervalo.
- uma estimativa pontual é uma estimativa de valor único de um parâmetro. Por exemplo, uma média de amostra é uma estimativa pontual de uma média populacional.
- uma estimativa de intervalo fornece um intervalo de valores onde o parâmetro deve estar. Um intervalo de confiança é o tipo mais comum de estimativa de intervalo.
ambos os tipos de estimativas são importantes para reunir uma ideia clara de onde um parâmetro provavelmente se encontra.
