az átlag standard hibája, vagy egyszerűen standard hiba, azt jelzi, hogy a populáció átlaga valószínűleg mennyire különbözik a minta átlagától. Megmutatja, hogy a minta átlaga mennyiben változna, ha egy vizsgálatot egyetlen populáción belüli új minták felhasználásával ismételne meg.
az átlag standard hibája (SE vagy SEM) a standard hiba leggyakrabban jelentett típusa. De megtalálhatja a standard hibát más statisztikákhoz is, például a mediánokhoz vagy az arányokhoz. A standard hiba a mintavételi hiba általános mértéke—a populációs paraméter és a mintastatisztika közötti különbség.
miért számít a standard hiba
a statisztikákban a mintákból származó adatokat használják a nagyobb populációk megértésére. A Standard hiba azért fontos, mert segít megbecsülni, hogy a mintaadatok mennyire képviselik a teljes populációt.
valószínűségi mintavétellel, ahol a minta elemeit véletlenszerűen választják ki, olyan adatokat gyűjthet, amelyek valószínűleg reprezentatívak a sokaságra. Azonban még valószínűségi mintákkal is, néhány mintavételi hiba marad. Ez azért van, mert egy minta soha nem fog tökéletesen illeszkedni ahhoz a populációhoz, amelyből származik, például az eszközök és a szórások szempontjából.
a standard hiba kiszámításával megbecsülheti, hogy a minta mennyire reprezentatív a populációban, és érvényes következtetéseket vonhat le.
egy magas standard hiba azt mutatja, hogy a minta átlaga széles körben elterjedt a populáció átlagában—a minta nem feltétlenül képviseli szorosan a populációt. Az alacsony standard hiba azt mutatja, hogy a mintaeszközök szorosan eloszlanak a populáció átlagában-a minta reprezentatív a populációra.
a minta méretének növelésével csökkentheti a standard hibát. Nagy, véletlenszerű minta használata a legjobb módszer a mintavételi torzítás minimalizálására.
Standard hiba vs szórás
a Standard hiba és a szórás mind a variabilitás mértéke:
- a szórás egyetlen mintán belüli variabilitást ír le.
- a standard hiba a populáció több mintájának variabilitását becsüli meg.


a szórás egy leíró statisztika, amely a mintaadatokból kiszámítható. Ezzel szemben a standard hiba egy következtetési statisztika, amely csak becsülhető (kivéve, ha a valós populációs paraméter ismert).
a matematikai pontszámok szórása 180. Ez a szám átlagosan azt tükrözi, hogy az egyes pontszám mennyiben különbözik az 550-es minta átlagos pontszámától.
a matematikai pontszámok standard hibája viszont megmutatja, hogy az 550-es minta átlagos pontszáma mennyiben különbözik a többi minta átlagos pontszámától, azonos méretű mintákban, a régió összes tesztelőjének populációjában.
Standard hiba képlet
az átlag standard hibáját a szórás és a minta nagysága alapján számítják ki.
a képletből látni fogja, hogy a minta mérete fordítottan arányos a standard hibával. Ez azt jelenti, hogy minél nagyobb a minta, annál kisebb a standard hiba, mert a minta statisztikája közelebb kerül a populációs paraméter megközelítéséhez.
különböző képleteket használunk attól függően, hogy a populáció szórása ismert-e. Ezek a képletek több mint 20 elemet tartalmazó mintáknál működnek (n > 20).
ha a populációs paraméterek ismertek
ha a populáció szórása ismert, akkor az alábbi képletben felhasználhatja a standard hiba pontos kiszámításához.
| képlet | magyarázat |
|---|---|
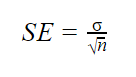 |
|
ha a populációs paraméterek ismeretlenek
ha a populációs szórás ismeretlen, akkor az alábbi képletet csak a standard hiba becslésére használhatja. Ez a képlet a minta szórását a populáció szórásának pontbecsléseként veszi figyelembe.
| képlet | magyarázat |
|---|---|
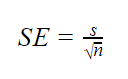 |
|
először keresse meg a minta méretének négyzetgyökét (n).
| képlet | számítás |
|---|---|
| √n | n = 200
ons = √200 = 14.1 |
ezután ossza el a minta szórását az első lépésben talált számmal.
| képlet | számítás |
|---|---|
| S = S = n | s = 180
ca = 14,1 s CA 6437= 180 ÷ 14.1 = 12.8 |
a matematikai SAT pontszámok standard hibája 12,8.
hogyan kell jelenteni a standard hibát?
jelentheti a standard hibát az átlag mellett vagy egy konfidencia intervallumban, hogy közölje az átlag körüli bizonytalanságot.
a standard hiba jelentésének legjobb módja a megbízhatósági intervallum, mert az olvasóknak nem kell további matematikát végezniük ahhoz, hogy értelmes intervallumot hozzanak létre.
a konfidencia intervallum olyan értéktartomány, ahol egy ismeretlen populációs paraméter várhatóan az idő nagy részében fekszik, ha új véletlenszerű mintákkal ismételné meg a vizsgálatot.
95% – os konfidencia szint mellett az összes minta átlagának 95% – a várhatóan a konfidencia intervallumon belül lesz a minta átlagának 1,96 standard hibája.
véletlenszerű mintavétel alapján a valódi populációs paraméter is becslések szerint 95% – os megbízhatósággal ebbe a tartományba esik.
egy normálisan elosztott jellemző esetében, mint például a SAT pontszámok, az összes minta átlagának 95% – a A minta átlagának nagyjából 4 standard hibájába esik.
| konfidencia intervallum képlet | |
|---|---|
|
CI = x 6 (1,96 se) x = Minta átlag = 550 |
|
| alsó határ | felső határ |
|
x – (1.96 ons) 550 − (1.96 × 12.8) = 525 |
x + (1.96 6 .. se) 550 + (1.96 × 12.8) = 575 |
véletlenszerű mintavétel esetén a 95% – os CI azt mondja, hogy 0,95 valószínűsége van annak, hogy a populáció átlagos matematikai SAT-pontszáma 525 és 575 között van.
Egyéb standard hibák
az átlag (és más statisztikák) standard hibáján kívül két másik standard hiba is előfordulhat: a becslés standard hibája és a standard mérési hiba.
a becslés standard hibája a regresszióanalízishez kapcsolódik. Ez tükrözi a becsült regressziós egyenes körüli változékonyságot és a regressziós modell pontosságát. A becslés standard hibájának felhasználásával elkészítheti a valódi regressziós együttható konfidencia intervallumát.
a standard mérési hiba a mérés megbízhatóságáról szól. Azt jelzi, hogy a teszt mérési hibája mennyire változó, és gyakran jelentik a szabványosított tesztelés során. A standard mérési hiba felhasználható egy elem vagy egyén valódi pontszámának megbízhatósági intervallumának létrehozására.
Gyakran Ismételt Kérdések a standard hibáról
az átlag standard hibája, vagy egyszerűen standard hiba, azt jelzi, hogy a populáció átlaga valószínűleg mennyire különbözik a minta átlagától. Megmutatja, hogy a minta átlaga mennyiben változna, ha egy vizsgálatot egyetlen populáción belüli új minták felhasználásával ismételne meg.
a Standard hiba és a szórás egyaránt a variabilitás mértéke. A szórás a mintán belüli változékonyságot tükrözi, míg a standard hiba megbecsüli a populáció mintáinak változékonyságát.
leíró és következtetési statisztikák segítségével kétféle becslést készíthet a sokaságról: pontbecsléseket és intervallumbecsléseket.
- a pontbecslés egy paraméter egyetlen értékbecslése. Például a minta átlaga a populáció átlagának pontbecslése.
- az intervallumbecslés olyan értéktartományt ad meg, ahol a paraméter várhatóan fekszik. A konfidencia intervallum az intervallumbecslés leggyakoribb típusa.
mindkét típusú becslés fontos ahhoz, hogy világos képet kapjunk arról, hogy egy paraméter valószínűleg hol fekszik.
