hogyan lehet kiszámítani a P értéket Excel-ben?

Tartalom

1. 1. Mi A P-Érték?
   2. Miért Van Szükségünk A P-Értékre?
   3. Hol Használjuk A P Értéket A Való Életben?
      • Marketing
      • valószínűség
   4. hogyan lehet kiszámítani a P-értéket Excel-ben?
   5. utolsó szavak

mi a P érték?

a P-érték egy statisztikai kifejezés, amely segít meghatározni, hogy az alkalmazott hipotézis igaz-e, a mintavételi variáció valószínűsége. Egyszerűen elmondja nekünk, hogy mekkora az esélye ezeknek az eredményeknek, ha nullhipotézisünk igaz.

• a nullhipotézis olyan hipotézis, amely azt állítja, hogy a kapott eredményeket tiszta szerencse okozza.
• egy alternatív hipotézis azt állítja, hogy az eredmények kapunk nem szerencse, de vannak külső elemek, amelyek befolyásolják az eredményeket.

ez egy nagyon fontos és általánosan használt statisztikai kifejezés, és könnyen kiszámítható az olyan adatelemző programokban, mint a Microsoft Excel. Ebben a cikkben megtudhatja, hogyan használjuk, hol használjuk, és hogyan tudjuk kiszámítani az Excelben különböző módon.

kezdjük!

Miért Van Szükségünk A P-Értékre?

nagy populációkkal végzett kutatások során ki kell számítania az egyes egyének statisztikáit. De még ilyen esetben sem lehet biztos abban, hogy véletlen vagy egyszerűen szerencse miatt történt-e valami, mivel lehetetlen mindent megfigyelni. Itt jönnek be a statisztikák.

a statisztikai számítások nem adnak abszolút igazságot, de segítenek abban, hogy jó ötleted legyen a kutatásokról.

a P-érték lehetővé teszi számunkra, hogy teszteljük a hipotézist a témánkban. Összehasonlíthatjuk a matematikai eredményeket ezekkel a hipotézisekkel, és újragondolhatjuk az utunkat anélkül, hogy sok időt töltenénk a kutatásban.

Hol Használjuk A P Értéket A Való Életben?

a valószínűségi értéket használjuk, ahol megpróbálunk tesztelni egy hipotézist. Ez lehet a kutatásról vagy egy egyszerű fogadásról, amelyet barátunkkal tettünk.

könnyebb megérteni példákkal.

Marketing:

tegyük fel, hogy a marketing területén dolgozik, és a legutóbbi projektje a gabonafélék reklámozásával foglalkozik.

készített egy videót a közösségi média számára, és megkapta az információkat, hogy a felhasználók inkább kihagyták vagy hosszú ideig nézték.

például a videó közös nézési ideje 20 másodperc. Az átlag 20 másodperc. Te pedig úgy döntöttél, hogy egy darab vidámabb zenével szerkeszted a videót.

most hogyan fogja felismerni, ha működött? Ezen a ponton szignifikancia statisztikákat használunk.

először állítson elő egy nullhipotézist:

a nullhipotézis azt állítja, hogy nincs összefüggés a befektetett és az elért eredmények között. Ez nem befolyásolja az eredményeket.

ebben a példában a nullhipotézis a következő lesz: “nincs kapcsolat az óraidőre alkalmazott változások között.”

ezután az alternatív hipotézis:

az alternatív hipotézis azt sugallja, hogy valójában a zene megváltoztatása működött, és most az emberek több mint 20 másodpercig nézik a reklámot. Matematikailag az alternatív hipotézis szerint:

” az átlag meghaladja a 20 másodpercet.”

Számítsa ki a szignifikancia szintet:

most be kell állítanunk egy határküszöböt annak kiszámításához, hogy sikeresek vagyunk-e vagy sem. Ezt szignifikancia szintnek nevezik, amelyet alfa értéknek is neveznek. Ez lehet bármilyen százalékos szeretne, ez teljesen rajtad múlik.

de ebben a példában 0,05 lesz.

most, hogy biztosan kiszámítsuk, mindig meg kell adnunk az összes nézési időt. De az Ön idejét és forrásait tekintve mintát kell vennie a lakosságból:

1. 100 emberből vett mintát.
2. ennek a 100 embernek 25 másodperces nézési ideje van a reklámhoz.
3. ez azt jelenti, hogy a minta átlaga 25.

ez a számítás nagyon egyszerű változata. De a minta szórását általában ebben a skálán számítják ki, ha nem ismeri a teljes populáció szórását.

használhatja a mintához kiszámított értékeket, mivel azok közel vannak a sokaság értékeihez. A minta átlaga közel áll a populáció átlagához.

Számítsa ki a P-értéket:

a p-érték megmutatja, hogy elutasíthatjuk-e a nullhipotézist vagy sem. Az a valószínűség, hogy a minta átlaga nagyobb vagy egyenlő 25 perc, figyelembe véve a nullhipotézist, igaz.

két helyzet fordulhat elő.

1. ha a p-érték kisebb, mint az alfa, akkor elutasíthatja a nullhipotézist. Statisztikai bizonyíték van arra, hogy az alternatív hipotézis igaz.
2. de ha a p-érték nagyobb vagy egyenlő az alfával, akkor nem utasíthatja el a nullhipotézist. Ez nem azt jelenti, hogy a nullhipotézis minden bizonnyal igaz, de nem is kerülhető el.

valószínűség

dolgozzunk egy másik példán.

a barátod és te dobd érme a levegőben: ha ez írás elveszíti 5 dollárt, és ha jön fej nyersz 5 dollárt.

• a barátod fejtetőre az érme egyszer: jön a farok. Ez rendben van, van egy 50% esély arra, hogy jön a farok. Most feltételezzük, hogy a valószínűsége 0,5, mert úgy gondolja, hogy ez egy tisztességes érme. Ez a nullhipotézised.

• második: ez farok. Elvesztettél egy másik 5 dollárt, de ez rendben van, mert még mindig van egy jó esély a két farok egy sorban. A p-érték 0,25, és ez még mindig tisztességes Arány.
• harmadik: ismét farok. A farok esélye háromszor egymás után 0,12. Ez nem alacsony, így nincs elég bizonyíték arra, hogy a nullhipotézis nem helyes. De elkezdi azt gondolni, hogy az alternatív hipotézise helyes lehet.
• negyedik: kiderül, mint farok újra látni fogja, hogy az esélye egyre nagyon alacsony. Ez lehet egy csodálatos véletlen, de még mindig van egy 0,6 esély, és még mindig nincs elég bizonyíték, hogy támogassa az alternatív hipotézist, hogy azt mondja, az érme trükkös. És várja meg az ötödik fordulót.
• ötödik: ez farok. Annak az esélye, hogy egy érme kiderül, mint farok ötször egymás után 0,3 ami nagyon alacsony. Ez az a pont, ahol elutasíthatja a nullhipotézist, mert nincs elég bizonyíték annak alátámasztására.

megkéred a barátodat, hogy nézze meg az érmét, és amikor megfogod, rájössz, hogy két farka van, és ez egy trükkös érme.

mi okozta, hogy elveszítjük a nullhipotézisünkbe vetett hitünket?

egy tisztességes játék essek érmék, az esélye, hogy egy fej vagy a farok 50%. Ez egy olyan helyzet, amikor úgy gondoljuk, hogy az érme tisztességes, de mivel a p-érték csökken, a hipotézisbe vetett bizalmunk is gyengült.

kevés esély van véletlenszerű farokra, ha a p-érték 0,05 alá csökken. Tehát, ha ezt a statisztikai kifejezést olyan kérdésekre alkalmazzuk, mint a rákkutatás vagy az éghajlatváltozás hatásai, akkor nagyobb jelentőséget kap.

 megjegyzés: nincs konkrét ok használjuk 0,05 p-érték alapértelmezett számítás. A képlet készítője úgy döntött, hogy ez egy jó szám a számításhoz, és az alapértelmezett számítások ragaszkodnak hozzá. 0,05 azt jelenti, 5% - ban 100 egyének populációk, amely beleesik a normál görbe. Ez az egyik oka annak, hogy általánosan használják. Ha meg akarja változtatni a számítás során, akkor megteheti.

hogyan lehet kiszámítani a P-értéket Excel-ben?

a P-érték kiszámításának több módja is van a Microsoft Excelben. Akkor írja le képletek vagy használhatja Analysis ToolPak. Ez a cikk tartalmazza, hogyan kell csinálni mindkét irányban.

a klasszikus Excel képletek használata:

kezdjük a klasszikus Excel képlettel. Két módja van ennek a TDIST-képletnek és a T-teszt képletnek.

1.1) TDIST képlet

először is szüksége lesz egy adatkészletre a p-érték kiszámításához.

• tegyük fel, hogy Ön tanár, és össze szeretné hasonlítani, hogy a diákok mit szereztek az utolsó vizsgán, és mit vártak a pontszámuk alapján az előző vizsgák alapján.
• megvan az eredmény 25, 46, 34, 27, 35, 43, 40, 44, 21 és 39 a legutóbbi vizsgádra.
• most a számításhoz szüksége van egy másik farokra, ez az a pontszám, amelyet a korábbi tesztek alapján vártál: 23, 44, 32, 20, 46, 37, 35, 42, 33, és 35

most, hogy a p-érték képletet Excelben használhassuk, előzetesen ki kell számolnunk néhány dolgot:

Pearson-együttható (r): Ez egy statisztikai kifejezés, amely két adat közötti lineáris korrelációt méri. A p-érték kiszámításához nem kell ismernie annak matematikai aspektusát. A következő bekezdésekben látni fogja az egyszerű képletet.

népesség (n): n az adathalmazban lévő személyek teljes száma.

T statisztika: az adatok becsült értékének a feltételezett értéktől a standard hibához viszonyított eltérésének aránya.

szabadságfok: az adathalmazban lévő egyének száma mínusz kettő.

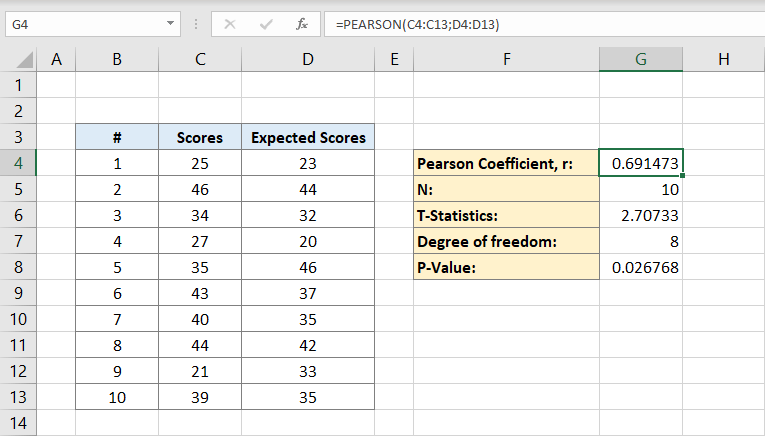
ebben a példában a Pearson-együtthatót az F4-re írják. Miután rákattintott, írja be a következő képletet:

a C oszlopok a pontszámokra, a D oszlopok pedig a várt pontszámokra vonatkoznak. A Pearson-együttható ebben a példában 0,691473.

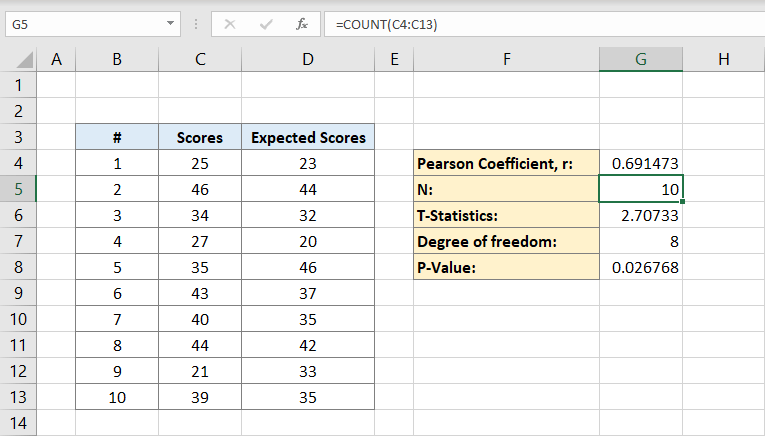
Ezután írja be az egyének számát az adatkészletbe. Ha biztosan tudja, hogy hány egyén van, akkor manuálisan is beírhatja, de ha nem, akkor használhatja a képletet:

miért tartalmaz a képlet csak C oszlopot?

ez azért van, mert csak akkor kell az egyének egy adathalmaz kiszámításához ezért egy oszlop fog tenni. A G5 cella most tartalmazza a 10-es számot. Ez a mi lakosságunk.

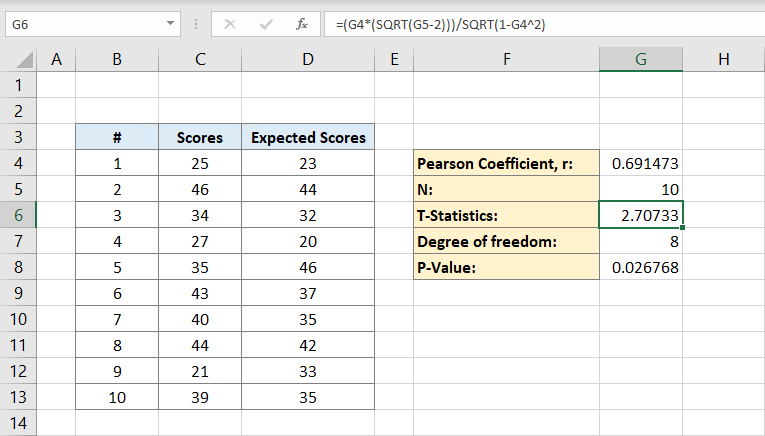
most, hogy megvan mind a Pearson-együttható, mind a populáció, kiszámíthatja a T statisztikát. A matematikai képlet t statisztika a Pearson-együttható (r) szorjel négyzetgyöke népesség (n) mínusz 2 osztva 1 négyzetgyökével mínusz Pearson-együttható négyzet:

a g6 cella tartalmazza az eredményt 2,70733. Ez a mi t statisztikánk.

ezt követően kiszámítja a szabadság mértékét. Írja be:

a G7 cellába. Ez a szabadság mértéke. 8-kor lesz.

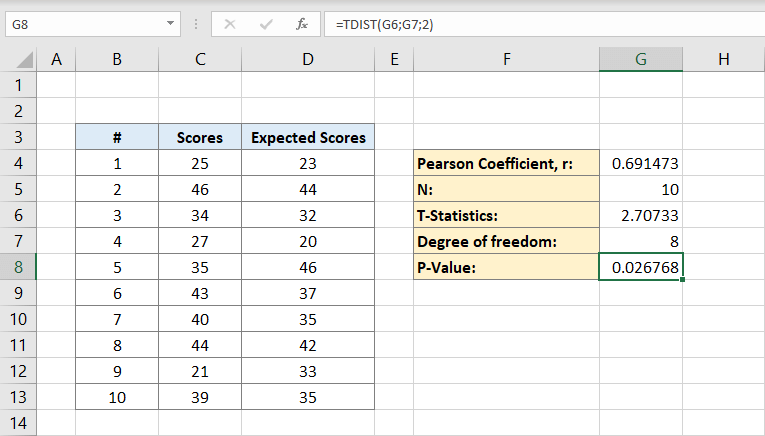
most már minden, amire szüksége van a P-érték kiszámításához. A G8 cella tartalmazza a képletet. Vagyis:

vagy

az eredmény 0,026768 lesz. Ez az adatkészlet p-értéke.

1.2. T-teszt képlet

a P-érték Excel képletekkel történő meghatározásának második módja a T-teszt képlet használata. Kicsit hasonlít az előző példához, de rövidebb.

• tegyük fel, hogy az adatkészlet ugyanaz, megvan az eredmény 25, 46, 34, 27, 35,43, 40, 44, 21, 39 a legutóbbi vizsgádhoz.
• várható eredmények 23, 44, 32, 20, 46, 37, 35, 42, 33, 35.
• hozzá fog adni egy harmadik oszlopot a várható és a tényleges pontszám közötti különbséghez. A különbség oszlopban 2, 2, 2, 7, 11, 6, 5, 2, 12, 4 az E4-től az E13-ig íródik.

most írja be a T-tesztet az E8 cellába. A T-teszt képletet a mellette lévő üres cellába fogja írni. Azaz:

ez a képlet közvetlenül megadja a p-értéket.

határozza meg a P-érték Excel eszköz Pak

vette Pak egy csomag, amely lehetővé teszi, hogy kiszámítja a különböző statisztikai mérések automatikusan, így könnyű és nagyon praktikus. Ez is könnyen telepíthető.

1. lépés: Menjen a beállításokhoz. A bal sarok alján található egy” Bővítmények ” gomb, kattintson rá. Megjelenik egy új ablak, keresse meg az “Analysis Tool Pak” opciót, kattintson rá, majd kattintson az ablak alján található go gombra.

2.lépés: aktiválja a bővítményt a mellette lévő pipa szimbólumra, majd a jobb oldali oszlop OK gombjára kattintva.

3. lépés: ha sikerült megfelelően aktiválnia, a munkalap felső menüjében a jobb oldalon megjelenik az” adatelemzés ” gomb.

4. lépés: Kattintson az” adatelemzés “gombra, és válassza a” t-teszt: két minta párosítása az eszközökhöz ” lehetőséget. Ezután kattintson az OK gombra. Megjelenik egy új ablak.

5. lépés: megkérdezi a bemeneteket az ablak első sorában. C4 típus: C13 a “változó 1 tartomány” mezőbe. Írja be a D4: D13 szót a” változó 2 tartomány ” mezőbe. Hagyja az alfa mezőt Az alapértelmezett értékkel.

6. lépés: az ablak második sorában kiválaszthatja, hogy hol figyelje az eredményeket. Ez lehet egy új munkalap vagy bármilyen üres cella. Ha azt szeretné, hogy az eredmény egy cellában legyen, győződjön meg róla, hogy lezárja az oszlopot és a sort. Ezután kattintson az OK gombra.

 tipp: Használja a dollárjelet a betű és a szám előtt az oszlop és a sor lezárásához. Ha például A2 cellát szeretne lezárni, írja be a $a$2 értéket.

7. lépés: az Excel kiszámítja az átlagot, a varianciát, a megfigyeléseket, a Pearson-korrelációt, a feltételezett átlagos különbséget, a T statisztikát, a p-értéket és így tovább.

záró szavak

a P-érték könnyen kiszámítható és sokféle helyzetben alkalmazható. Segít abban, hogy megkapja a szükséges információkat anélkül, hogy sok időt vagy erőfeszítést költene rá. Még könnyebb kiszámítani, ha olyan statisztikai elemző programokat használ, mint a Microsoft Excel, amelyek a megfelelő eszközökkel és képletekkel rendelkeznek. Nézzük meg a Someka sablonok gyűjteményét, és töltsünk le statisztikai sablonokat, hogy megkönnyítsük a munkáját!

kapcsolódó olvasmányok:

• hogyan lehet kiszámítani a konfidencia intervallumot Excel – ben?
• Elemezheti Az Excel Az Adatokat?