a statisztikában négy adat mérési skála létezik: névleges, ordinális, intervallum és Arány. Ezek egyszerűen a különböző típusú adatok kategorizálásának módjai (itt található a statisztikai adattípusok áttekintése) . Ezt a témát általában az akadémiai oktatás összefüggésében, ritkábban a “Való Világban” tárgyalják.”Ha ezt a fogalmat statisztikai tesztre készíti, Köszönje meg Stanley Stevens nevű pszichológus kutatónak, hogy előállt ezekkel a kifejezésekkel.
ezt a négy adatmérési skálát (névleges, sorszám, intervallum és arány) a legjobban a példával lehet megérteni, amint azt alább láthatja.
névleges
kezdjük a legkönnyebben érthető. A névleges skálákat a változók címkézésére használják, mennyiségi érték nélkül. A “névleges” skálákat egyszerűen “címkéknek” lehet nevezni.”Íme néhány példa az alábbiakban. Figyeljük meg, hogy ezek a skálák kölcsönösen kizárják egymást (nincs átfedés), és egyiküknek sincs numerikus jelentősége. Egy jó módja annak, hogy emlékezzen mindezt ,hogy a” névleges “hangzik, mint a” név “és névleges skála olyan, mint a” nevek ” vagy címkék.
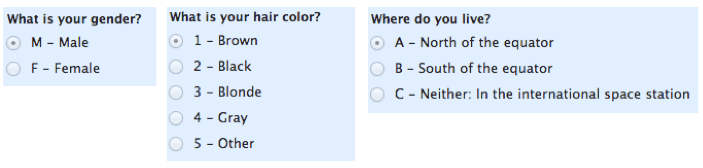
Megjegyzés: A Névleges skála altípusát, amelynek csak két kategóriája van (pl. férfi/nő), “dichotómnak” nevezzük.”Ha diák vagy, ezt felhasználhatod arra, hogy lenyűgözd a tanárodat.
Bónusz Megjegyzés #2: A névleges adatok egyéb altípusai a ” névleges sorrendben “(például” hideg, meleg, forró, nagyon forró”) és a névleges sorrend nélkül (például”férfi/nő”).
Ordinal
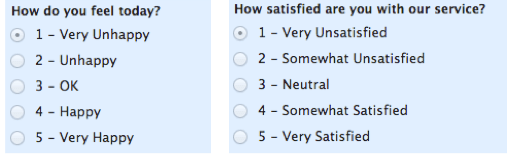
ordinal skálák esetén az értékek sorrendje az, ami fontos és jelentős, de az egyes értékek közötti különbségek nem igazán ismertek. Vessen egy pillantást az alábbi példára. Mindegyik esetben tudjuk, hogy a #4 jobb, mint a #3 vagy # 2, de nem tudjuk–és nem tudjuk számszerűsíteni–, hogy mennyivel jobb. Például, a különbség az “OK” és a “boldogtalan” között ugyanaz, mint a “nagyon boldog” és a “boldog” között?”Nem tudjuk megmondani.
az ordinális skálák általában nem numerikus fogalmak, például elégedettség, boldogság, kellemetlenség stb.
az”Ordinal” könnyen megjegyezhető, mert úgy hangzik, mint a “rend”, és ez a legfontosabb, hogy emlékezzen a “ordinal scales”–re-ez a sorrend, ami számít, de ez minden, amit igazán kapsz ezekből.
haladó megjegyzés: a sorszámadatok halmazán a központi tendencia meghatározásának legjobb módja a mód vagy a medián használata; egy purista elmondja, hogy az átlag nem határozható meg sorszámkészletből.
intervallum
az Intervallumskálák olyan numerikus skálák, amelyekben ismerjük mind az értékek sorrendjét, mind a pontos különbségeket. Az intervallum skála klasszikus példája a Celsius hőmérséklet, mivel az egyes értékek közötti különbség azonos. Például a 60 és 50 fok közötti különbség mérhető 10 fok, csakúgy, mint a 80 és 70 fok közötti különbség.
az Intervallumskálák szépek, mert megnyílik a statisztikai elemzés ezen adatkészleteken. Például a központi tendencia móddal, mediánnal vagy átlaggal mérhető; a szórás is kiszámítható.
a többiekhez hasonlóan elég könnyen emlékezhet az “intervallum skála” legfontosabb pontjaira. Maga az” intervallum “azt jelenti, hogy” tér a kettő között”, amire fontos emlékezni–az intervallum skálák nemcsak a sorrendről, hanem az egyes elemek közötti értékről is mesélnek nekünk.
itt van a probléma az intervallum skálákkal: nincs “valódi nulla.”Például nincs olyan, hogy “nincs hőmérséklet”, legalábbis celsius-nál nem. Intervallumskálák esetén a nulla nem jelenti az érték hiányát, hanem valójában egy másik szám, amelyet a skálán használnak, például 0 celsius fok. A negatív számoknak is van jelentése. Valódi nulla nélkül lehetetlen kiszámítani az arányokat. Az intervallumadatokkal összeadhatjuk és kivonhatjuk, de nem szorozhatjuk vagy oszthatjuk.
zavaros? Ok, fontolja meg ezt: 10 fok C + 10 fok C = 20 fok C. nincs probléma. A 20 C fok azonban nem kétszer olyan forró, mint a 10 C fok, mert a Celsius-skálán nincs olyan “hőmérséklet”. Fahrenheit-re konvertálva egyértelmű: 10C=50f és 20c=68F, ami nyilvánvalóan nem kétszer olyan forró. Remélem, van értelme. A lényeg az, hogy az intervallum skálák nagyszerűek, de nem tudjuk kiszámítani az arányokat, ami az utolsó mérési skálánkhoz vezet…

Arány
az Arányskálák a végső nirvána, amikor az adatmérési skálákról van szó, mert elmondják nekünk a sorrendet, megmondják az egységek közötti pontos értéket, és abszolút nulla is van–ami lehetővé teszi mind a leíró, mind a következtetési statisztikák széles skáláját. Azzal a kockázattal, hogy megismétlem magam, minden, ami az intervallumadatokról szól, az arányskálákra vonatkozik, a plusz arányskálák egyértelműen meghatározzák a nullát. Az arányváltozók jó példái közé tartozik a magasság, a súly és az időtartam.
az Arányskálák rengeteg lehetőséget kínálnak a statisztikai elemzéshez. Ezek a változók értelmesen hozzáadhatók, kivonhatók, szorozhatók, oszthatók (arányok). A központi tendenciát mód, medián vagy átlag segítségével lehet mérni; a diszperzió mértéke, például a szórás és a variációs együttható az arányskálákból is kiszámítható.

Összegzés
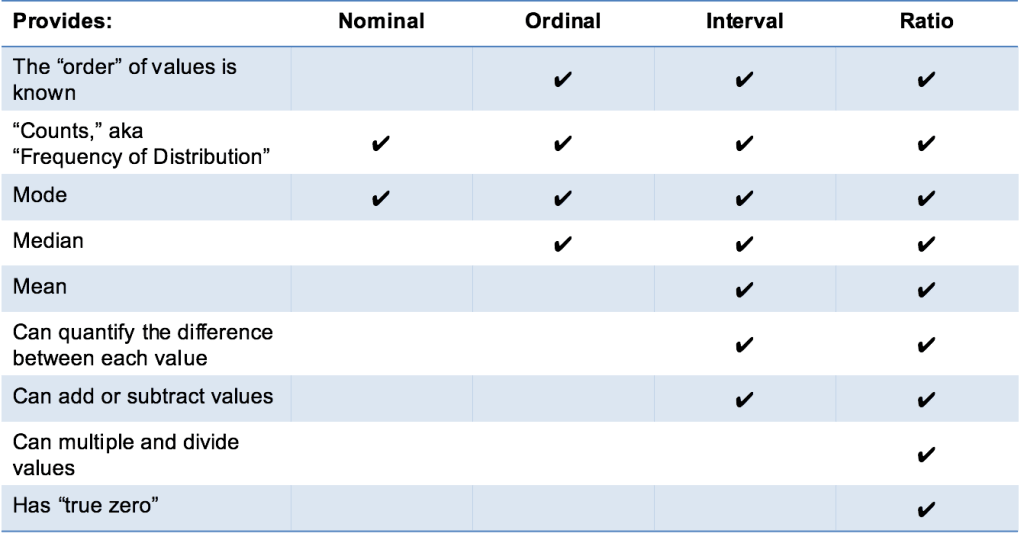
ennyi! Remélem, ez a magyarázat világos, és hogy tudod megérteni a négy típusú adatok mérési skálák: névleges, ordinális, intervallum, és Arány! Kapd el őket!
ha tesztelni szeretné képességeit ,adja meg az alábbi rövid kvízt (nem működik? Próbálja ki az asztali böngészőt):