En estadística, hay cuatro escalas de medición de datos: nominal, ordinal, intervalo y relación. Estas son simplemente formas de subcategorizar diferentes tipos de datos (aquí hay una descripción general de los tipos de datos estadísticos) . Este tema se discute generalmente en el contexto de la enseñanza académica y con menos frecuencia en el «mundo real».»Si está repasando este concepto para una prueba de estadísticas, agradezca a un investigador psicólogo llamado Stanley Stevens por proponer estos términos.
Estas cuatro escalas de medición de datos (nominal, ordinal, intervalo y relación) se entienden mejor con un ejemplo, como verá a continuación.
Nominal
Comencemos con la más fácil de entender. Las escalas nominales se utilizan para etiquetar variables, sin ningún valor cuantitativo. Las escalas » nominales «podrían llamarse simplemente «etiquetas».»Aquí hay algunos ejemplos, a continuación. Observe que todas estas escalas son mutuamente excluyentes (no se superponen) y ninguna de ellas tiene importancia numérica. Una buena manera de recordar todo esto es que «nominal» suena mucho a «nombre» y las escalas nominales son como «nombres» o etiquetas.
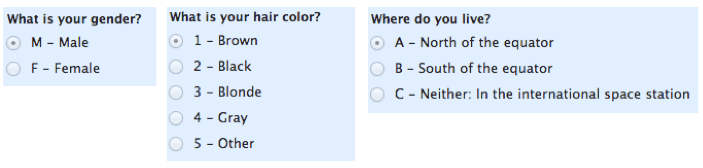
Nota: un subtipo de escala nominal con solo dos categorías (por ejemplo, masculino/femenino) se denomina «dicotómico.»Si eres un estudiante, puedes usar eso para impresionar a tu maestro.
Nota de bonificación # 2: Otros subtipos de datos nominales son «nominales con orden» (como «frío, cálido, caliente, muy caliente») y nominales sin orden (como «hombre/mujer»).
Ordinal
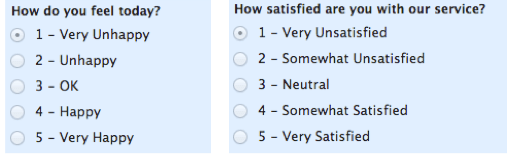
Con las escalas ordinales, el orden de los valores es lo importante y significativo, pero las diferencias entre cada una no se conocen realmente. Echa un vistazo al siguiente ejemplo. En cada caso, sabemos que un #4 es mejor que un #3 o #2, pero no sabemos–y no se puede cuantificar cuánto mejor es. Por ejemplo, ¿la diferencia entre «OK» e «Infeliz» es la misma que la diferencia entre «Muy Feliz» y «Feliz»?»No podemos decirlo.
Las escalas ordinales son típicamente medidas de conceptos no numéricos como satisfacción, felicidad, incomodidad, etc.
» Ordinal «es fácil de recordar porque suena como» orden «y esa es la clave para recordar con»escalas ordinales»: es el orden lo que importa, pero eso es todo lo que realmente obtienes de estas.
Avanzado Nota: La mejor manera de determinar la tendencia central en un conjunto de datos ordinales es usar el modo o mediana; un purista le dirá que la media no se puede definir a partir de un conjunto ordinal.
Intervalo
Las escalas de intervalos son escalas numéricas en las que conocemos tanto el orden como las diferencias exactas entre los valores. El ejemplo clásico de una escala de intervalos es la temperatura Celsius porque la diferencia entre cada valor es la misma. Por ejemplo, la diferencia entre 60 y 50 grados es de 10 grados medibles, al igual que la diferencia entre 80 y 70 grados.
Las escalas de intervalos son agradables porque se abre el campo del análisis estadístico de estos conjuntos de datos. Por ejemplo, la tendencia central se puede medir por modo, mediana o media; también se puede calcular la desviación estándar.
Al igual que los demás, puede recordar los puntos clave de una «escala de intervalos» con bastante facilidad. «Intervalo» en sí significa «espacio intermedio», lo que es importante recordar: las escalas de intervalos no solo nos informan sobre el orden, sino también sobre el valor entre cada elemento.
Este es el problema con las escalas de intervalos: no tienen un «cero verdadero».»Por ejemplo, no hay tal cosa como «sin temperatura», al menos no con grados celsius. En el caso de las escalas de intervalos, cero no significa la ausencia de valor, sino que en realidad es otro número utilizado en la escala, como 0 grados celsius. Los números negativos también tienen significado. Sin un cero verdadero, es imposible calcular las proporciones. Con los datos de intervalo, podemos sumar y restar, pero no podemos multiplicar ni dividir.
Confundido? Bien, considera esto: 10 grados C + 10 grados C = 20 grados C. No hay problema. 20 grados C no es el doble de caliente que 10 grados C, sin embargo, porque no hay tal cosa como «sin temperatura» cuando se trata de la escala Celsius. Cuando se convierte a Fahrenheit, está claro: 10C = 50F y 20C = 68F, que claramente no es el doble de caliente. Espero que tenga sentido. En resumen, las escalas de intervalos son excelentes, pero no podemos calcular las proporciones, lo que nos lleva a nuestra última escala de medición…

Relación
Las escalas de relación son el nirvana definitivo cuando se trata de escalas de medición de datos porque nos dicen sobre el orden, nos dicen el valor exacto entre unidades Y también tienen un cero absoluto, lo que permite aplicar una amplia gama de estadísticas descriptivas e inferenciales. A riesgo de repetirme, todo lo anterior sobre los datos de intervalos se aplica a las escalas de cocientes, además las escalas de cocientes tienen una definición clara de cero. Entre los buenos ejemplos de variables de relación se incluyen la altura, el peso y la duración.
Las escalas de cocientes proporcionan una gran cantidad de posibilidades cuando se trata de análisis estadístico. Estas variables se pueden sumar, restar, multiplicar, dividir de manera significativa (ratios). La tendencia central se puede medir por modo, mediana o media; las medidas de dispersión, como la desviación estándar y el coeficiente de variación, también se pueden calcular a partir de escalas de cocientes.

Resumen
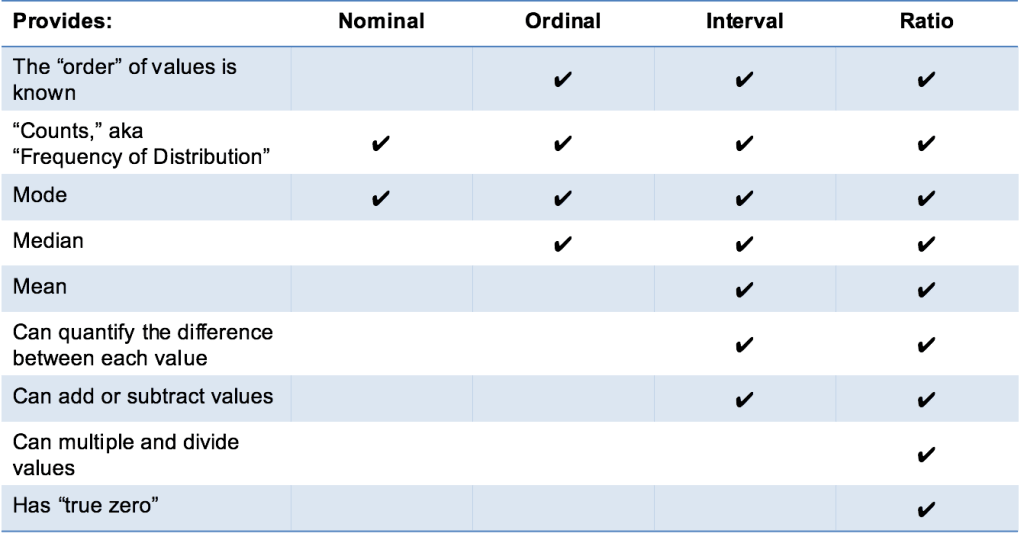
¡Eso es todo! Espero que esta explicación sea clara y que sepa comprender los cuatro tipos de escalas de medición de datos: nominal, ordinal, intervalo y relación. ¡Ve por ellos!
Si desea poner a prueba sus habilidades, pruebe el breve cuestionario a continuación (¿no funciona? Probar en un navegador de escritorio):