El error estándar de la media, o simplemente error estándar, indica cuán diferente es probable que sea la media de la población de una media de muestra. Le indica cuánto variaría la media de la muestra si tuviera que repetir un estudio utilizando muestras nuevas de una sola población.
El error estándar de la media (SE o SEM) es el tipo de error estándar más comúnmente notificado. Pero también puedes encontrar el error estándar para otras estadísticas, como medianas o proporciones. El error estándar es una medida común de error de muestreo, la diferencia entre un parámetro de población y una estadística de muestra.
Por qué importa el error estándar
En las estadísticas, los datos de las muestras se utilizan para comprender poblaciones más grandes. El error estándar es importante porque le ayuda a estimar qué tan bien los datos de muestra representan a toda la población.
Con el muestreo probabilístico, en el que los elementos de una muestra se seleccionan al azar, puede recopilar datos que probablemente sean representativos de la población. Sin embargo, incluso con muestras probabilísticas, algunos errores de muestreo permanecerán. Esto se debe a que una muestra nunca coincidirá perfectamente con la población de la que proviene en términos de medidas como medias y desviaciones estándar.
Al calcular el error estándar, puede estimar cuán representativa es su muestra de su población y sacar conclusiones válidas.
Un error estándar alto muestra que las medias de la muestra están ampliamente distribuidas alrededor de la media de la población; es posible que su muestra no represente de cerca a su población. Un error estándar bajo muestra que las medias de la muestra están muy distribuidas alrededor de la media de la población: su muestra es representativa de su población.
Puede disminuir el error estándar aumentando el tamaño de la muestra. El uso de una muestra grande y aleatoria es la mejor manera de minimizar el sesgo de muestreo.
Error estándar vs desviación estándar
El error estándar y la desviación estándar son medidas de variabilidad:
- La desviación estándar describe la variabilidad dentro de una sola muestra.
- El error estándar estima la variabilidad entre múltiples muestras de una población.


La desviación estándar es una estadística descriptiva que se puede calcular a partir de datos de muestra. Por el contrario, el error estándar es una estadística inferencial que solo se puede estimar (a menos que se conozca el parámetro de población real).
La desviación estándar de los puntajes matemáticos es 180. Este número refleja en promedio cuánto difiere cada puntaje de la puntuación media de la muestra de 550.
El error estándar de las puntuaciones matemáticas, por otro lado, indica en qué medida la puntuación media de la muestra de 550 difiere de otras puntuaciones medias de la muestra, en muestras de igual tamaño, en la población de todos los candidatos a exámenes en la región.
Fórmula de error estándar
El error estándar de la media se calcula utilizando la desviación estándar y el tamaño de la muestra.
De la fórmula, verá que el tamaño de la muestra es inversamente proporcional al error estándar. Esto significa que cuanto mayor sea la muestra, menor será el error estándar, porque la estadística de la muestra estará más cerca de acercarse al parámetro de población.
Se utilizan diferentes fórmulas dependiendo de si se conoce la desviación estándar de la población. Estas fórmulas funcionan para muestras con más de 20 elementos (n > 20).
Cuando se conocen parámetros de población
Cuando se conoce la desviación estándar de la población, puede usarla en la fórmula siguiente para calcular el error estándar con precisión.
| Fórmula | Explicación |
|---|---|
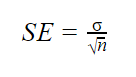 |
|
Cuando los parámetros de población son desconocidos
Cuando la desviación estándar de la población es desconocida, puede usar la fórmula siguiente para estimar solo el error estándar. Esta fórmula toma la desviación estándar de la muestra como estimación puntual de la desviación estándar de la población.
| Fórmula | Explicación |
|---|---|
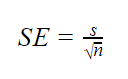 |
|
En primer lugar, busque la raíz cuadrada de su tamaño de muestra (n).
| Cálculo de fórmula | |
|---|---|
| √n | n = 200
√n = √200 = 14.1 |
A continuación, divida la desviación estándar de la muestra por el número que encontró en el paso uno.
| Fórmula | Cálculo |
|---|---|
| SE = s ÷ √n | s = 180
√n = 14.1 s ÷ √n = 180 ÷ 14.1 = 12.8 |
El error estándar de matemáticas en los puntajes del SAT es de 12.8.
¿Cómo debe informar el error estándar?
Puede informar el error estándar junto con la media o en un intervalo de confianza para comunicar la incertidumbre alrededor de la media.
La mejor manera de informar el error estándar es en un intervalo de confianza, ya que los lectores no tendrán que hacer cálculos adicionales para llegar a un intervalo significativo.
Un intervalo de confianza es un rango de valores en el que se espera que se encuentre un parámetro de población desconocido la mayor parte del tiempo, si tuviera que repetir su estudio con nuevas muestras aleatorias.
Con un nivel de confianza del 95%, se espera que el 95% de todas las medias de la muestra se encuentren dentro de un intervalo de confianza de ± 1,96 errores estándar de la media de la muestra.
Sobre la base de un muestreo aleatorio, también se estima que el parámetro de población verdadera se encuentra dentro de este rango con una confianza del 95%.
Para una característica normalmente distribuida, como las puntuaciones SAT, el 95% de todas las medias de la muestra están dentro de aproximadamente 4 errores estándar de la media de la muestra.
| Fórmula de intervalo de confianza | |
|---|---|
|
IC = x ± (1,96 × SE) x = media muestral = 550 |
|
| Límite inferior | Límite superior |
|
x – (1.96 × SE) 550 − (1.96 × 12.8) = 525 |
x + (1,96 × SE) 550 + (1.96 × 12.8) = 575 |
Con el muestreo aleatorio, un IC del 95% indica que hay una probabilidad de 0,95 de que la puntuación media del SAT en matemáticas de la población esté entre 525 y 575.
Otros errores estándar
Aparte del error estándar de la media (y otras estadísticas), hay otros dos errores estándar que puede encontrar: el error estándar de la estimación y el error estándar de medición.
El error estándar de la estimación está relacionado con el análisis de regresión. Esto refleja la variabilidad alrededor de la línea de regresión estimada y la precisión del modelo de regresión. Usando el error estándar de la estimación, puede construir un intervalo de confianza para el coeficiente de regresión verdadero.
El error estándar de medición se refiere a la fiabilidad de una medida. Indica cuán variable es el error de medición de una prueba, y a menudo se informa en pruebas estandarizadas. El error estándar de medición se puede utilizar para crear un intervalo de confianza para la puntuación verdadera de un elemento o un individuo.
Preguntas frecuentes sobre error estándar
El error estándar de la media, o simplemente el error estándar, indica cuán diferente es probable que sea la media de la población de una media de la muestra. Le indica cuánto variaría la media de la muestra si tuviera que repetir un estudio utilizando muestras nuevas de una sola población.
El error estándar y la desviación estándar son medidas de variabilidad. La desviación estándar refleja la variabilidad dentro de una muestra, mientras que el error estándar estima la variabilidad entre muestras de una población.
Utilizando estadísticas descriptivas e inferenciales, puede hacer dos tipos de estimaciones sobre la población: estimaciones puntuales y estimaciones de intervalos.
- Una estimación puntual es una estimación de valor única de un parámetro. Por ejemplo, una media muestral es una estimación puntual de una media poblacional.
- Una estimación de intervalo le da un rango de valores donde se espera que se encuentre el parámetro. Un intervalo de confianza es el tipo más común de estimación de intervalos.
Ambos tipos de estimaciones son importantes para obtener una idea clara de dónde es probable que se encuentre un parámetro.
