L’erreur-type de la moyenne, ou simplement erreur-type, indique à quel point la moyenne de la population est susceptible d’être différente d’une moyenne d’échantillon. Il vous indique dans quelle mesure la moyenne de l’échantillon varierait si vous deviez répéter une étude en utilisant de nouveaux échantillons provenant d’une seule population.
L’erreur-type de la moyenne (SE ou SEM) est le type d’erreur-type le plus souvent signalé. Mais vous pouvez également trouver l’erreur standard pour d’autres statistiques, comme les médianes ou les proportions. L’erreur type est une mesure courante de l’erreur d’échantillonnage — la différence entre un paramètre de population et une statistique d’échantillon.
Pourquoi l’erreur-type est importante
En statistiques, les données provenant d’échantillons sont utilisées pour comprendre les populations plus importantes. L’erreur type est importante car elle vous aide à estimer dans quelle mesure vos données d’échantillon représentent l’ensemble de la population.
Avec l’échantillonnage probabiliste, où les éléments d’un échantillon sont sélectionnés au hasard, vous pouvez collecter des données susceptibles d’être représentatives de la population. Cependant, même avec des échantillons probabilistes, une erreur d’échantillonnage subsistera. En effet, un échantillon ne correspondra jamais parfaitement à la population dont il provient en termes de mesures telles que les moyennes et les écarts types.
En calculant l’erreur type, vous pouvez estimer la représentativité de votre échantillon de votre population et tirer des conclusions valables.
Une erreur type élevée montre que les moyennes de l’échantillon sont largement réparties autour de la moyenne de la population — votre échantillon peut ne pas représenter étroitement votre population. Une erreur type faible montre que les moyennes de l’échantillon sont étroitement réparties autour de la moyenne de la population — votre échantillon est représentatif de votre population.
Vous pouvez réduire l’erreur type en augmentant la taille de l’échantillon. L’utilisation d’un grand échantillon aléatoire est le meilleur moyen de minimiser le biais d’échantillonnage.
Erreur-type par rapport à l’écart-type
L’erreur-type et l’écart-type sont deux mesures de variabilité:
- L’écart type décrit la variabilité au sein d’un seul échantillon.
- L’erreur type estime la variabilité entre plusieurs échantillons d’une population.


L’écart type est une statistique descriptive qui peut être calculée à partir de données d’échantillon. En revanche, l’erreur type est une statistique inférentielle qui ne peut être qu’estimée (à moins que le paramètre de population réelle ne soit connu).
L’écart type des scores mathématiques est de 180. Ce nombre reflète en moyenne dans quelle mesure chaque score diffère du score moyen de l’échantillon de 550.
L’erreur type des scores mathématiques, en revanche, vous indique dans quelle mesure le score moyen de l’échantillon de 550 diffère des autres scores moyens de l’échantillon, dans des échantillons de taille égale, dans la population de tous les candidats de la région.
Formule d’erreur type
L’erreur type de la moyenne est calculée à l’aide de l’écart type et de la taille de l’échantillon.
À partir de la formule, vous verrez que la taille de l’échantillon est inversement proportionnelle à l’erreur type. Cela signifie que plus l’échantillon est grand, plus l’erreur type est petite, car la statistique de l’échantillon sera plus proche du paramètre de population.
Différentes formules sont utilisées selon que l’écart type de population est connu ou non. Ces formules fonctionnent pour des échantillons avec plus de 20 éléments (n > 20).
Lorsque les paramètres de population sont connus
Lorsque l’écart-type de population est connu, vous pouvez l’utiliser dans la formule ci-dessous pour calculer précisément l’erreur-type.
| Formule | Explication |
|---|---|
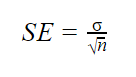 |
|
Lorsque les paramètres de population sont inconnus
Lorsque l’écart-type de population est inconnu, vous pouvez utiliser la formule ci-dessous pour estimer uniquement l’erreur-type. Cette formule prend l’écart-type de l’échantillon comme estimation ponctuelle de l’écart-type de la population.
| Formule | Explication |
|---|---|
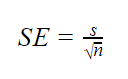 |
|
Tout d’abord, trouvez la racine carrée de la taille de votre échantillon (n).
| Formule | Calcul |
|---|---|
| √ n | n = 200
√n = √200 = 14.1 |
Ensuite, divisez l’écart type de l’échantillon par le nombre que vous avez trouvé à la première étape.
| Formule | Calcul |
|---|---|
| SE = s ÷ √n | s = 180
√n = 14,1 s ÷ √n = 180 ÷ 14.1 = 12.8 |
L’erreur type des scores mathématiques SAT est de 12,8.
Comment devez-vous signaler l’erreur type?
Vous pouvez signaler l’erreur type à côté de la moyenne ou dans un intervalle de confiance pour communiquer l’incertitude autour de la moyenne.
La meilleure façon de signaler l’erreur type est dans un intervalle de confiance, car les lecteurs n’auront pas à faire de calculs supplémentaires pour trouver un intervalle significatif.
Un intervalle de confiance est une plage de valeurs où un paramètre de population inconnu devrait se situer la plupart du temps, si vous deviez répéter votre étude avec de nouveaux échantillons aléatoires.
Avec un niveau de confiance de 95 %, on s’attend à ce que 95 % de toutes les moyennes de l’échantillon se situent dans un intervalle de confiance de ± 1,96 erreurs-types de la moyenne de l’échantillon.
Sur la base d’un échantillonnage aléatoire, on estime également que le paramètre de population réelle se situe dans cette plage avec une confiance de 95 %.
Pour une caractéristique normalement distribuée, comme les scores SAT, 95 % de toutes les moyennes de l’échantillon se situent à environ 4 erreurs types de la moyenne de l’échantillon.
| Formule d’intervalle de confiance | |
|---|---|
|
CI = x ± (1,96 × SE) x = moyenne de l’échantillon = 550 |
|
| Limite inférieure | Limite supérieure |
|
x − (1.96 × SE) 550 − (1.96 × 12.8) = 525 |
x + (1,96 × SE) 550 + (1.96 × 12.8) = 575 |
Avec un échantillonnage aléatoire, un IC à 95% vous indique qu’il existe une probabilité de 0,95 que le score moyen de la population en mathématiques se situe entre 525 et 575.
Autres erreurs-types
Outre l’erreur-type de la moyenne (et d’autres statistiques), il existe deux autres erreurs-types que vous pourriez rencontrer : l’erreur-type de l’estimation et l’erreur-type de mesure.
L’erreur type de l’estimation est liée à l’analyse de régression. Cela reflète la variabilité autour de la ligne de régression estimée et la précision du modèle de régression. En utilisant l’erreur type de l’estimation, vous pouvez construire un intervalle de confiance pour le coefficient de régression vrai.
L’erreur type de mesure concerne la fiabilité d’une mesure. Il indique à quel point l’erreur de mesure d’un test est variable, et elle est souvent rapportée dans les tests standardisés. L’erreur type de mesure peut être utilisée pour créer un intervalle de confiance pour le score réel d’un élément ou d’un individu.
Foire aux questions sur l’erreur type
L’erreur-type de la moyenne, ou simplement erreur-type, indique à quel point la moyenne de la population est susceptible d’être différente d’une moyenne de l’échantillon. Il vous indique dans quelle mesure la moyenne de l’échantillon varierait si vous deviez répéter une étude en utilisant de nouveaux échantillons provenant d’une seule population.
L’erreur-type et l’écart-type sont deux mesures de la variabilité. L’écart type reflète la variabilité au sein d’un échantillon, tandis que l’erreur type estime la variabilité entre les échantillons d’une population.
En utilisant des statistiques descriptives et inférentielles, vous pouvez faire deux types d’estimations sur la population: les estimations ponctuelles et les estimations d’intervalles.
- Une estimation ponctuelle est une estimation de valeur unique d’un paramètre. Par exemple, une moyenne d’échantillon est une estimation ponctuelle d’une moyenne de population.
- Une estimation d’intervalle vous donne une plage de valeurs où le paramètre est censé se trouver. Un intervalle de confiance est le type d’estimation d’intervalle le plus courant.
Les deux types d’estimations sont importants pour avoir une idée claire de l’emplacement probable d’un paramètre.
