ve statistice existují čtyři stupnice měření dat: nominální, pořadové, intervalové a poměr. Jedná se jednoduše o způsoby, jak podkategorizovat různé typy dat (zde je přehled statistických datových typů) . Toto téma je obvykle diskutováno v kontextu akademické výuky a méně často v “ reálném světě.“Pokud jste oprášili tento koncept pro statistický test, děkuji psychologovi výzkumníkovi jménem Stanley Stevens za to, že přišel s těmito podmínkami.
tyto čtyři stupnice měření dat (nominální, ordinální, interval a poměr) jsou nejlépe pochopeny na příkladu, jak uvidíte níže.
nominální
začněme nejjednodušším pochopením. Jmenovité stupnice se používají pro označování proměnných bez jakékoli kvantitativní hodnoty. „Nominální“ váhy lze jednoduše nazvat “ štítky.“Zde jsou některé příklady, níže. Všimněte si, že všechny tyto stupnice se vzájemně vylučují (bez překrytí) a žádná z nich nemá žádný číselný význam. Dobrý způsob, jak si to všechno pamatovat, je, že „nominální“ zní hodně jako „jméno“ a nominální stupnice jsou něco jako „jména“ nebo štítky.
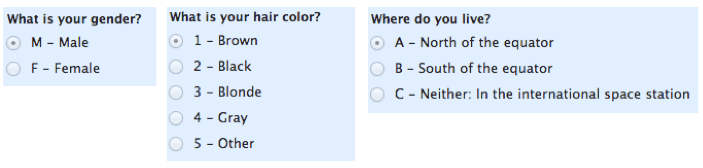
Poznámka: podtyp Jmenovité stupnice pouze se dvěma kategoriemi (např. muž/žena) se nazývá „dichotomický“.“Pokud jste student, můžete to použít k zapůsobení na svého učitele.
Bonusová Poznámka #2: Jiné podtypy nominálních dat jsou „nominální s řádem“ (jako „studený, teplý, horký, velmi horký“) a nominální bez pořadí (jako „muž/žena“).
Ordinal
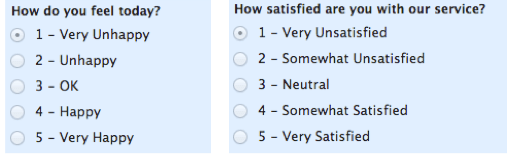
u pořadových stupnic je pořadí hodnot to, co je důležité a významné, ale rozdíly mezi nimi nejsou ve skutečnosti známy. Podívejte se na níže uvedený příklad. V každém případě víme, že a # 4 je lepší než a #3 nebo #2, ale nevíme–a nemůžeme kvantifikovat-o kolik je lepší. Například, je rozdíl mezi “ OK “ a “ nešťastný „stejný jako rozdíl mezi“ velmi šťastný „a“ šťastný?“Nemůžeme říct.
pořadové stupnice jsou obvykle měřítky nečíselných pojmů, jako je spokojenost, štěstí, nepohodlí atd.
„Ordinal“ je snadno zapamatovatelný, protože zní jako „ordinal“ a to je klíč k zapamatování s „ordinal scales“ – je to pořadí, na čem záleží–ale to je vše, co z nich opravdu získáte.
upřesnit poznámka: nejlepší způsob, jak určit centrální tendenci na množině pořadových dat, je použít režim nebo medián; purista vám řekne, že průměr nelze definovat z řadové množiny.
Interval
intervalové stupnice jsou číselné stupnice, ve kterých známe pořadí i přesné rozdíly mezi hodnotami. Klasickým příkladem intervalové stupnice je teplota Celsia, protože rozdíl mezi každou hodnotou je stejný. Například rozdíl mezi 60 a 50 stupni je měřitelný 10 stupňů, stejně jako rozdíl mezi 80 a 70 stupni.
intervalové stupnice jsou pěkné, protože se otevírá oblast statistické analýzy těchto datových sad. Například centrální tendenci lze měřit režimem, mediánem nebo průměrem; lze také vypočítat směrodatnou odchylku.
stejně jako ostatní si můžete snadno zapamatovat klíčové body „intervalové stupnice“. „Interval“ sám o sobě znamená „prostor mezi“, což je důležité si pamatovat–intervalové stupnice nám nejen říkají o pořadí, ale také o hodnotě mezi jednotlivými položkami.
zde je problém s intervalovými stupnicemi: nemají “ skutečnou nulu.“Například neexistuje žádná taková věc jako „žádná teplota“ , alespoň ne s celsius. V případě intervalových stupnic nula neznamená absenci hodnoty,ale je to vlastně další číslo použité na stupnici, jako 0 stupňů Celsia. Záporná čísla mají také význam. Bez skutečné nuly není možné vypočítat poměry. S daty intervalu můžeme sčítat a odečítat, ale nemůžeme násobit ani dělit.
zmatený? Dobře, zvažte toto: 10 stupňů C + 10 stupňů C = 20 stupňů C. žádný problém. 20 stupňů C však není dvakrát tak horké jako 10 stupňů C, protože pokud jde o stupnici Celsia, neexistuje nic jako „žádná teplota“. Při převodu na Fahrenheit je jasné: 10C=50F a 20C=68F, což zjevně není dvakrát tak horké. Doufám, že to dává smysl. Sečteno a podtrženo, intervalové stupnice jsou skvělé, ale nemůžeme vypočítat poměry, což nás přivádí k naší poslední měřící stupnici…

poměr
Poměrové stupnice jsou konečnou Nirvanou, pokud jde o stupnice měření dat, protože nám říkají o pořadí, říkají nám přesnou hodnotu mezi jednotkami a mají také absolutní nulu–což umožňuje použití široké škály popisných i inferenčních statistik. S rizikem opakování se vše výše o intervalových datech vztahuje na poměrné stupnice, plus poměrné stupnice mají jasnou definici nuly. Dobré příklady proměnných poměru zahrnují výšku, hmotnost a trvání.
poměr váhy poskytují nepřeberné množství možností, pokud jde o statistické analýzy. Tyto proměnné lze smysluplně sčítat, odečítat, násobit, dělit (poměry). Centrální tendenci lze měřit režimem, mediánem nebo průměrem; míry rozptylu, jako je směrodatná odchylka a variační koeficient, lze také vypočítat z poměrových stupnic.

shrnutí
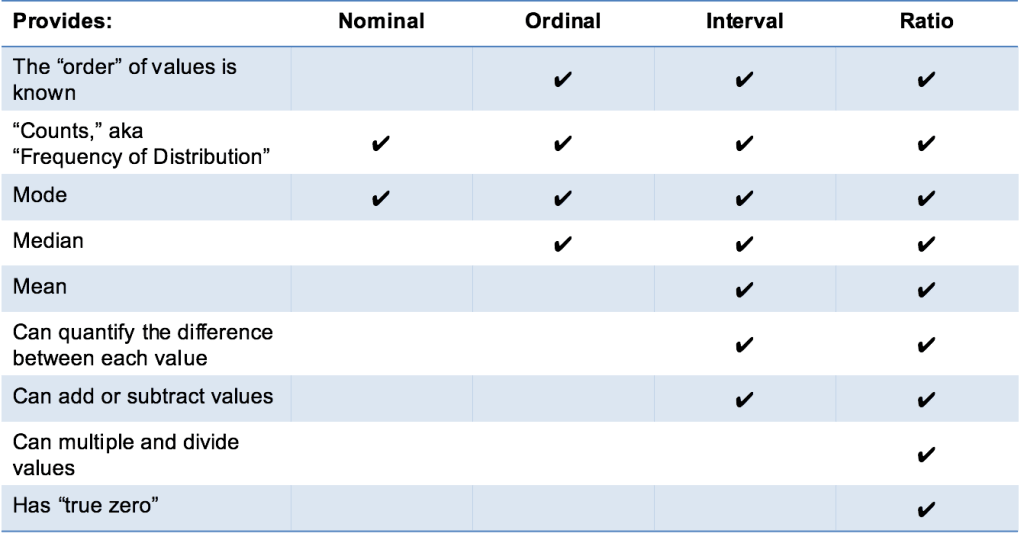
a je to! Doufám, že toto vysvětlení je jasné a že víte, že rozumíte čtyřem typům měřítek měření dat: nominální, pořadové, intervalové a poměr! Běž pro ně!
pokud si chcete vyzkoušet své dovednosti, dejte krátký kvíz pod go (nefunguje? Zkuste na stolním prohlížeči):