standardní chyba průměru nebo jednoduše standardní chyba označuje, jak odlišný je průměr populace pravděpodobně od průměru vzorku. Říká vám, jak moc by se průměr vzorku lišil, kdybyste zopakovali studii s použitím nových vzorků z jedné populace.
standardní chyba průměru (SE nebo SEM) je nejčastěji hlášeným typem standardní chyby. Standardní chybu ale najdete i u jiných statistik, jako jsou mediány nebo proporce. Standardní chyba je běžná míra chyby vzorkování-rozdíl mezi parametrem populace a statistikou vzorku.
proč standardní chyba záleží
ve statistikách se data ze vzorků používají k pochopení větších populací. Standardní chyba záleží, protože vám pomůže odhadnout, jak dobře vaše vzorová data představují celou populaci.
při vzorkování pravděpodobnosti, kde jsou prvky vzorku náhodně vybrány, můžete shromažďovat data, která budou pravděpodobně reprezentativní pro populaci. I u pravděpodobnostních vzorků však zůstane určitá chyba vzorkování. Je to proto, že vzorek nikdy nebude dokonale odpovídat populaci, ze které pochází, pokud jde o opatření, jako jsou prostředky a směrodatné odchylky.
výpočtem standardní chyby můžete odhadnout, jak reprezentativní je váš vzorek vaší populace, a učinit platné závěry.
vysoká standardní chyba ukazuje, že prostředky vzorku jsou široce rozšířeny kolem průměru populace-váš vzorek nemusí přesně reprezentovat vaši populaci. Nízká standardní chyba ukazuje, že prostředky vzorku jsou úzce rozděleny kolem průměru populace – váš vzorek je reprezentativní pro vaši populaci.
můžete snížit standardní chybu zvýšením velikosti vzorku. Použití velkého náhodného vzorku je nejlepší způsob, jak minimalizovat zkreslení vzorkování.
standardní chyba vs směrodatná odchylka
standardní chyba a směrodatná odchylka jsou obě měřítka variability:
- směrodatná odchylka popisuje variabilitu v rámci jednoho vzorku.
- standardní chyba odhaduje variabilitu napříč více vzorky populace.


směrodatná odchylka je popisná statistika, kterou lze vypočítat ze vzorových dat. Naproti tomu standardní chyba je inferenční statistika, kterou lze odhadnout pouze (pokud není znám parametr skutečné populace).
směrodatná odchylka matematických skóre je 180. Toto číslo v průměru odráží, jak moc se každé skóre liší od průměrného skóre vzorku 550.
standardní chyba matematických skóre vám naproti tomu říká, jak moc se průměrné skóre vzorku 550 liší od ostatních průměrných skóre vzorku ve vzorcích stejné velikosti v populaci všech účastníků testu v regionu.
standardní chybový vzorec
standardní chyba průměru se vypočítá pomocí směrodatné odchylky a velikosti vzorku.
ze vzorce uvidíte, že velikost vzorku je nepřímo úměrná standardní chybě. To znamená, že čím větší je vzorek, tím menší je standardní chyba, protože statistika vzorku bude blíže blížící se parametru populace.
používají se různé vzorce v závislosti na tom, zda je známa směrodatná odchylka populace. Tyto vzorce pracují pro vzorky s více než 20 prvky (n > 20).
jsou-li známy parametry populace
je-li známa směrodatná odchylka populace, můžete ji použít v níže uvedeném vzorci k přesnému výpočtu standardní chyby.
| vzorec | vysvětlení |
|---|---|
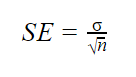 |
|
pokud nejsou známy parametry populace
pokud není známa směrodatná odchylka populace, můžete použít níže uvedený vzorec pouze k odhadu standardní chyby. Tento vzorec bere směrodatnou odchylku vzorku jako bodový odhad směrodatné odchylky populace.
| vzorec | vysvětlení |
|---|---|
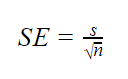 |
|
nejprve najděte druhou odmocninu velikosti vzorku (n).
| vzorec | výpočet |
|---|---|
| √n | n = 200
√n = √200 = 14.1 |
dále vydělte směrodatnou odchylku vzorku číslem, které jste našli v prvním kroku.
| vzorec | výpočet |
|---|---|
| se = s √√n | s = 180
√ n = 14.1 s ÷ √n = 180 ÷ 14.1 = 12.8 |
standardní chyba matematických SAT skóre je 12.8.
jak byste měli nahlásit standardní chybu?
standardní chybu můžete hlásit vedle střední hodnoty nebo v intervalu spolehlivosti, abyste sdělili nejistotu kolem střední hodnoty.
nejlepší způsob, jak nahlásit standardní chybu, je v intervalu spolehlivosti, protože čtenáři nebudou muset dělat žádnou další matematiku, aby přišli se smysluplným intervalem.
interval spolehlivosti je rozsah hodnot, kde se očekává, že neznámý parametr populace bude ležet většinu času, pokud byste měli opakovat studii s novými náhodnými vzorky.
při 95% úrovni spolehlivosti se očekává, že 95% všech prostředků vzorku bude ležet v intervalu spolehlivosti ± 1,96 standardních chyb průměru vzorku.
na základě náhodného odběru vzorků se odhaduje, že skutečný populační parametr leží v tomto rozmezí s 95% jistotou.
pro normálně distribuovanou charakteristiku, jako je skóre SAT, 95% všech prostředků vzorku spadá do zhruba 4 standardních chyb průměru vzorku.
| vzorec intervalu spolehlivosti | |
|---|---|
|
CI = x ± (1,96 × SE) x = průměr vzorku = 550 |
|
| dolní mez | horní mez |
|
x – (1.96 × SE) 550 − (1.96 × 12.8) = 525 |
x + (1,96 × SE) 550 + (1.96 × 12.8) = 575 |
při náhodném odběru vzorků vám 95% CI říká, že existuje pravděpodobnost 0,95, že průměrné skóre matematiky SAT v populaci je mezi 525 a 575.
ostatní standardní chyby
kromě standardní chyby průměru (a dalších statistik) můžete narazit na dvě další standardní chyby: standardní chybu odhadu a standardní chybu měření.
standardní chyba odhadu souvisí s regresní analýzou. To odráží variabilitu kolem odhadované regresní linie a přesnost regresního modelu. Pomocí standardní chyby odhadu můžete vytvořit interval spolehlivosti pro skutečný regresní koeficient.
standardní chyba měření se týká spolehlivosti opatření. Označuje, jak variabilní je chyba měření testu, a často se uvádí ve standardizovaném testování. Standardní chyba měření může být použita k vytvoření intervalu spolehlivosti pro skutečné skóre prvku nebo jednotlivce.
Časté dotazy týkající se standardní chyby
standardní chyba průměru nebo jednoduše standardní chyba označuje, jak odlišný je průměr populace od průměru vzorku. Říká vám, jak moc by se průměr vzorku lišil, kdybyste zopakovali studii s použitím nových vzorků z jedné populace.
standardní chyba a směrodatná odchylka jsou obě měřítka variability. Směrodatná odchylka odráží variabilitu ve vzorku, zatímco standardní chyba odhaduje variabilitu napříč vzorky populace.
pomocí popisných a inferenčních statistik můžete provést dva typy odhadů o populaci: bodové odhady a odhady intervalů.
- bodový odhad je odhad jedné hodnoty parametru. Například průměr vzorku je bodový odhad průměru populace.
- intervalový odhad vám dává rozsah hodnot, kde se očekává, že parametr bude ležet. Interval spolehlivosti je nejběžnějším typem odhadu intervalu.
oba typy odhadů jsou důležité pro získání jasné představy o tom, kde parametr pravděpodobně leží.
