Jak vypočítat hodnotu P v aplikaci Excel?

Obsah

1. 1. Jaká Je Hodnota P?
   2. Proč Potřebujeme Hodnotu P?
   3. Kde Používáme Hodnotu P V Reálném Životě?
      • Marketing
      • Pravděpodobnost
   4. Jak vypočítat hodnotu P v aplikaci Excel?
   5. závěrečná slova

jaká je hodnota P?

P-hodnota je statistický termín, který vám pomůže určit, zda je hypotéza, kterou používáte, pravdivá, pravděpodobnost variace vzorkování. Jednoduše nám říká, jaké jsou šance na získání těchto výsledků, pokud je naše nulová hypotéza pravdivá.

• nulová hypotéza je hypotéza, která tvrdí, že výsledky, které získáme, jsou způsobeny čistým štěstím.
• alternativní hypotéza tvrdí, že výsledky, které dostáváme, nejsou štěstí, ale existují vnější prvky, které ovlivňují naše výsledky.

je to velmi důležitý a běžně používaný statistický termín a lze jej snadno vypočítat v programech pro analýzu dat, jako je Microsoft Excel. V tomto článku se dozvíte, jak jej používáme, kde jej používáme a jak jej můžeme vypočítat v aplikaci Excel různými způsoby.

začněme!

Proč Potřebujeme Hodnotu P?

při výzkumu s velkou populací musíte vypočítat statistiky pro každého jednotlivce. Ale ani v takovém případě si nemůžete být jisti, zda se něco stalo kvůli náhodě nebo prostě štěstí, protože je nemožné vše pozorovat. Zde přicházejí statistiky.

statistické výpočty vám nemohou poskytnout absolutní pravdu, ale pomohou vám mít dobrou představu o vašich výzkumech.

P-hodnota nám umožňuje testovat hypotézu na našem předmětu. Můžeme porovnat matematické výsledky s těmito hypotézami a přehodnotit naši cestu, aniž bychom strávili velké množství času ve výzkumu.

Kde Používáme Hodnotu P V Reálném Životě?

použijeme hodnotu pravděpodobnosti, kde se pokusíme otestovat hypotézu. Může to být o výzkumu nebo jednoduché sázce, kterou jsme udělali s naším přítelem.

je snazší pochopit to s příklady.

Marketing:

řekněme, že pracujete v oblasti marketingu a váš nedávný projekt je v reklamě na obiloviny.

máte vytvořené video pro sociální média a máte informace pro uživatele, kteří je přeskočili nebo je dlouho sledovali.

jako příklad je běžná doba sledování videa 20 sekund. Průměr je 20 sekund. A rozhodli jste se upravit video s kusem radostnější hudby.

jak poznáte, zda to fungovalo? V tomto okamžiku používáme statistiku významnosti.

nejprve vytvořte nulovou hypotézu:

nulová hypotéza tvrdí, že neexistuje žádná korelace mezi tím, co investujete, a výsledky, které získáte. To nemá vliv na výsledky.

v tomto příkladu bude nulová hypotéza následující: „neexistuje žádný vztah mezi změnami, které aplikujete na čas sledování.“

pak alternativní hypotéza:

alternativní hypotéza naznačuje, že skutečně změna hudby fungovala a nyní lidé sledují reklamu déle než 20 sekund. Matematicky, alternativní hypotéza říká:

“ průměr je nyní větší než 20 sekund.“

Vypočítejte úroveň významnosti:

nyní musíme nastavit hraniční práh pro výpočet, zda jsme úspěšní nebo ne. Tomu se říká úroveň významnosti, která se navíc označuje jako hodnota alfa. Může to být libovolné procento, které byste chtěli, je to naprosto na vás.

ale během tohoto příkladu to bude 0,05.

nyní pro výpočet s jistotou bychom měli mít vždy všechna data času sledování. Ale pokud jde o váš čas a zdroje, měli byste vzít vzorek z populace:

1. odebrali jste vzorek 100 lidí.
2. těchto 100 lidí má 25 sekund času sledování reklamy.
3. znamená to, že průměr vzorku je 25.

Toto je velmi jednoduchá verze výpočtu. Směrodatná odchylka vzorku se však obvykle vypočítá v této stupnici, pokud neznáte směrodatnou odchylku celé populace.

můžete použít hodnoty, které jste vypočítali pro vzorek, protože se blíží populačním hodnotám. Průměr vzorku se blíží průměru populace.

Vypočítejte hodnotu P:

hodnota p nám ukazuje, zda můžeme nulovou hypotézu odmítnout nebo ne. Pravděpodobnost, že průměr vzorku je větší nebo roven 25 minutám vzhledem k nulové hypotéze, je pravdivá.

mohou nastat dvě situace.

1. pokud je hodnota p menší než alfa, můžete nulovou hypotézu odmítnout. Máte statistický důkaz, že alternativní hypotéza je pravdivá.
2. ale pokud je hodnota p větší nebo rovna alfa, nemůžete odmítnout nulovou hypotézu. Neznamená to, že nulová hypotéza je jistě pravdivá, ale také se jí nelze vyhnout.

Pravděpodobnost

pojďme pracovat na jiném příkladu.

váš přítel a vy jste hodili minci do vzduchu: pokud je to ocasy, ztratíte 5 dolarů a pokud to přijde, získáte 5 dolarů.

• váš přítel jednou hodí minci: přichází jako ocasy. To je v pořádku, tam je 50% šance, že to přijde jako ocasy. Nyní předpokládáte, že pravděpodobnost je 0,5, protože si myslíte, že je to spravedlivá mince. Toto je vaše nulová hypotéza.

• druhý: je to ocasy. Ztratili jste dalších 5 dolarů, ale je to v pořádku, protože stále existuje dobrá šance na dva ocasy v řadě. Hodnota p je 0,25 a je to stále spravedlivý poměr.
• třetí: je to opět ocasy. Šance na ocasy třikrát za sebou je 0,12. Není nízká, takže není dostatek důkazů, že nulová hypotéza není správná. Ale začnete si myslet, že vaše alternativní hypotéza by mohla být správná.
• čtvrtý: otočí se jako ocasy znovu uvidíte, jak jsou šance stále opravdu nízké. Může to být zázračná náhoda, ale stále existuje šance 0,6 a stále není dostatek důkazů na podporu alternativní hypotézy, která říká, že mince je složitá. A čekáte na pátý flip.
• pátý: je to ocasy. Šance na mince dopadá jako ocasy pětkrát za sebou je 0,3 což je velmi nízká. To je bod, který můžete odmítnout nulovou hypotézu, protože už není dostatek důkazů, které by ji podpořily.

požádáte svého přítele, aby viděl minci, a když ji držíte, uvědomíte si, že má dvě ocasy a je to složitá mince.

co způsobilo, že jsme ztratili víru v naši nulovou hypotézu?

ve spravedlivé hře obracení mincí je šance na získání hlavy nebo ocasu 50%. Toto je situace, kdy věříme, že mince je spravedlivá, ale jak hodnota p klesá, naše důvěra v tuto hypotézu také oslabila.

je malá šance na náhodné ocasy, když hodnota p klesne pod 0,05. Takže když použijete tento statistický termín v záležitostech, jako jsou výzkumy rakoviny nebo účinky změny klimatu, získává větší význam.

 Poznámka: neexistuje žádný konkrétní důvod, proč používáme 0,05 p-hodnota pro výchozí výpočet. Tvůrce vzorce se rozhodl, že je to dobré číslo pro výpočet a výchozí výpočty se s ním drží. 0,05 znamená 5% populace 100 jedinců, která spadá do normální křivky. To je jeden z důvodů, proč se běžně používá. Pokud ji chcete změnit během výpočtu sami, můžete.

Jak vypočítat hodnotu P v aplikaci Excel?

existuje více než jeden způsob, jak vypočítat hodnotu p v aplikaci Microsoft Excel. Můžete zadat vzorce nebo můžete použít analytický ToolPak. Tento článek obsahuje, jak to udělat oběma způsoby.

použití klasických vzorců Excel:

začněme klasickým způsobem vzorce Excel. Existují dva způsoby, jak to udělat TDIST vzorec a T-test vzorec.

1.1) TDIST vzorec

nejprve budete potřebovat datovou sadu pro výpočet hodnoty p.

• Řekněme, že jste učitel a chcete porovnat, co vaši studenti skórovali ve vaší poslední zkoušce a co jste očekávali, že jejich skóre bude založeno na jejich předchozích zkouškách.
• máte výsledky 25, 46, 34, 27, 35, 43, 40, 44, 21 a 39 za poslední zkoušku.
• nyní pro výpočet potřebujete další ocas, toto je skóre, které jste očekávali na základě předchozích testů: 23, 44, 32, 20, 46, 37, 35, 42, 33, a 35

nyní, abyste mohli použít vzorec hodnoty p v aplikaci Excel, měli byste předem vypočítat několik věcí:

Pearsonův koeficient (r): Jedná se o statistický termín, který měří lineární korelaci mezi dvěma daty. Pro výpočet hodnoty p nemusíte znát její matematický aspekt. V následujících odstavcích uvidíte jednoduchý vzorec.

populace (n): n je celkový počet osob ve vaší datové sadě.

t statistika: je to poměr odchylky odhadované hodnoty dat od její předpokládané hodnoty k její standardní chybě.

stupeň svobody: je to počet jednotlivců v datovém souboru minus dva.

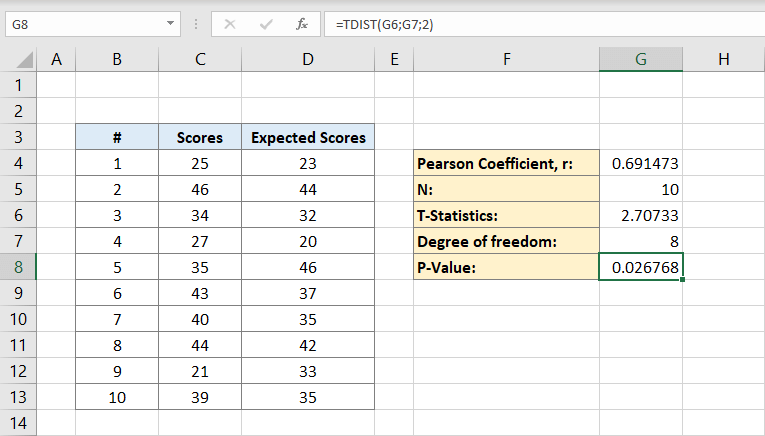
nyní bude Pearsonův koeficient zapsán na F4 v tomto příkladu. Po kliknutí na něj zadáte vzorec:

sloupce C jsou pro skóre a sloupce D jsou pro očekávané skóre. Pearsonův koeficient je v tomto příkladu 0,691473.

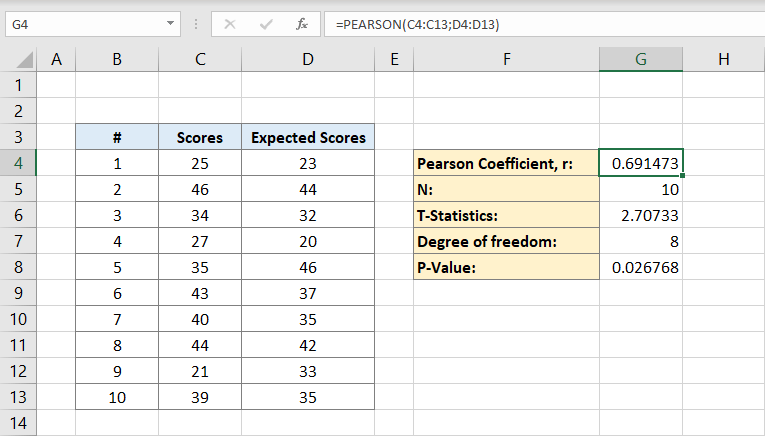
dále zadáte počet osob v datové sadě. Pokud jistě víte, kolik jednotlivců máte, můžete jej zadat ručně, ale pokud ne, můžete použít vzorec:

proč vzorec obsahuje pouze sloupec C?

je to proto, že potřebujeme pouze jednotlivce v jedné datové sadě pro výpočet proto jeden sloupec bude dělat. Buňka G5 bude nyní obsahovat číslo 10. Tohle je naše populace.

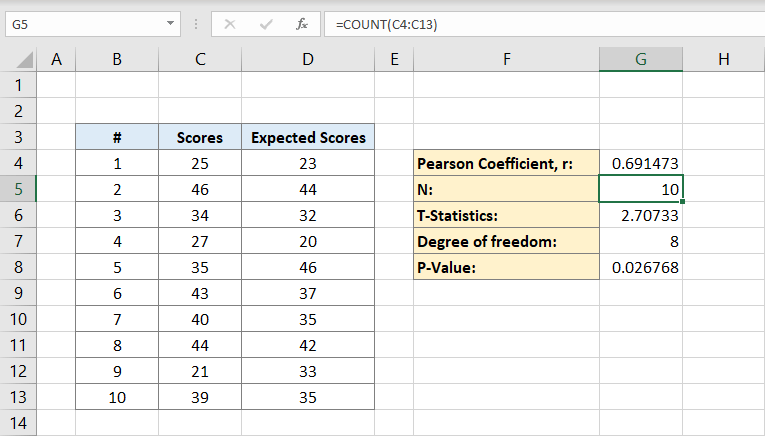
Nyní, když máte Pearsonův koeficient i populaci, můžete vypočítat statistiku T. Matematický vzorec pro statistiku T je Pearsonův koeficient (r) krát znaménko druhá odmocnina populace (n) minus 2 děleno druhou odmocninou z 1 minus Pearsonův koeficient na druhou:

buňka G6 bude obsahovat výsledek 2,70733. Toto je naše Statistika T.

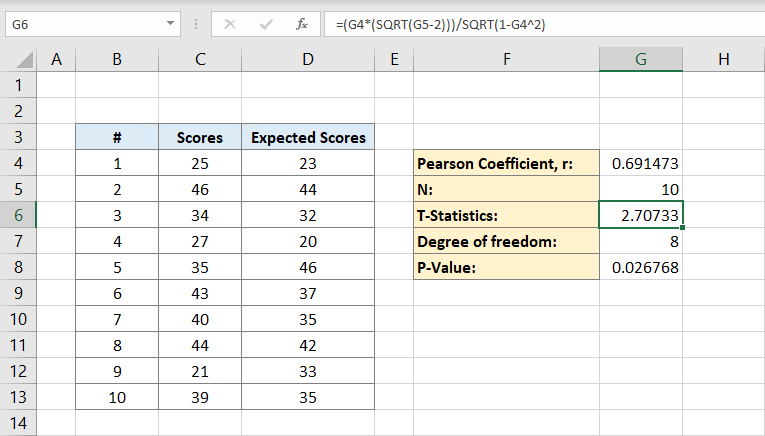
poté vypočítáte stupeň svobody. Do buňky G7 zadáte:

. To je míra svobody. Bude v 8.

Nyní máte vše, co potřebujete k výpočtu hodnoty P. Buňka G8 bude obsahovat vzorec. To znamená:

nebo

výsledek bude 0,026768. Toto je hodnota p pro datovou sadu.

1.2. T-Test Formula

druhým způsobem stanovení hodnoty p pomocí vzorců Excel je použití vzorce T-test. Je to trochu podobné předchozímu příkladu, ale kratší.

• řekněme, že datová sada je stejná, máte výsledky 25, 46, 34, 27, 35,43, 40, 44, 21, 39 na poslední zkoušku.
• očekávané výsledky jsou 23, 44, 32, 20, 46, 37, 35, 42, 33, 35.
• přidáte třetí sloupec pro rozdíl mezi očekávaným a skutečným skóre. Ve sloupci rozdíl 2, 2, 2, 7, 11, 6, 5, 2, 12, 4 bude psáno od E4 do E13.

Nyní zadejte T-Test do buňky E8. Napíšete vzorec T-testu do prázdné buňky vedle něj. To je:

a tento vzorec vám dá přímo hodnotu p.

určete hodnotu P pomocí nástroje Excel pak

pak je balíček, který umožňuje automaticky vypočítat různá statistická měření, takže je snadné a velmi užitečné. Je také snadná instalace.

Krok 1: Přejděte na Nastavení. V levém dolním rohu je tlačítko „doplňky“, klikněte na něj. Objeví se nové okno, najděte možnost „analytický nástroj Pak“, klikněte na něj a poté klikněte na tlačítko Přejít v dolní části okna.

Krok 2: aktivujte doplněk kliknutím na symbol zaškrtnutí vedle něj a za tlačítkem OK v pravém sloupci.

Krok 3: pokud se vám podařilo správně aktivovat tlačítko“ Analýza dat “ se objeví v horní nabídce listu na pravé straně.

Krok 4: Klikněte na tlačítko“ Analýza dat „a vyberte možnost“ t-Test: spárované Dva vzorky pro prostředky“. Poté klikněte na OK. Objeví se nové okno.

Krok 5: zeptá se vstupů v prvním řádku okna. Typ C4: C13 do pole“ rozsah proměnné 1″. Do pole „variable 2 range“ zadáte D4: D13. Ponechte pole alfa s výchozí hodnotou.

Krok 6: ve druhém řádku okna můžete vybrat, kde chcete sledovat výsledky. Může to být nový list nebo prázdné buňky. Pokud chcete výsledek na buňce, ujistěte se, že zamknete sloupec a řádek. Poté klikněte na tlačítko OK.

 Tip: Použijte znak dolaru před písmenem a číslem k uzamčení sloupce a řádku. Například pokud chcete zamknout buňku A2, zadejte $a$2.

Krok 7: Excel vypočítá průměr, rozptyl, pozorování, Pearsonovu korelaci, předpokládaný průměrný rozdíl, statistiku t, hodnotu p a další.

závěrečná slova

P-hodnota se snadno vypočítá a přizpůsobí v mnoha různých situacích. To vám pomůže získat informace, které potřebujete, aniž by trávit spoustu času nebo úsilí na to. Je ještě snazší vypočítat, když používáte programy statistické analýzy, jako je Microsoft Excel, které přicházejí se správnými nástroji a vzorci. Pojďme zkontrolovat sbírku šablon Someka a stáhnout statistické šablony, abychom vám usnadnili práci!

související údaje:

• Jak vypočítat interval spolehlivosti v aplikaci Excel?
• Může Excel Analyzovat Data?