błąd standardowy średniej, lub po prostu błąd standardowy, wskazuje, jak różna jest średnia populacji od średniej próby. Informuje o tym, jak bardzo średnia z próby zmieniłaby się, gdybyś powtórzył badanie z użyciem nowych próbek z jednej populacji.
błąd standardowy średniej (SE lub SEM) jest najczęściej zgłaszanym typem błędu standardowego. Ale można również znaleźć standardowy błąd dla innych statystyk, takich jak mediany lub proporcje. Błąd standardowy jest wspólną miarą błędu pobierania próbek-różnica między parametrem populacji i statystyki próby.
dlaczego błąd standardowy ma znaczenie
w statystykach dane z próbek są wykorzystywane do zrozumienia większych populacji. Błąd standardowy ma znaczenie, ponieważ pomaga oszacować, jak dobrze dane próbki reprezentują całą populację.
z próbkowania prawdopodobieństwa, gdzie elementy próbki są losowo wybrane, można zbierać dane, które mogą być reprezentatywne dla populacji. Jednak nawet w przypadku próbek prawdopodobieństwa, niektóre błędy próbkowania pozostaną. To dlatego, że próbka nigdy nie będzie idealnie pasować do populacji pochodzi z pod względem miar, takich jak średnie i odchylenia standardowe.
obliczając błąd Standardowy, możesz oszacować, jak reprezentatywna jest twoja próbka populacji i wyciągnąć prawidłowe wnioski.
błąd o wysokim standardzie pokazuje, że średnie próbki są szeroko rozpowszechnione wokół średniej populacji—twoja próbka może nie reprezentować twojej populacji. Niski błąd standardowy pokazuje, że środki próbki są ściśle rozmieszczone wokół średniej populacji-próbka jest reprezentatywna dla populacji.
możesz zmniejszyć standardowy błąd, zwiększając rozmiar próbki. Korzystanie z dużej, losowej próbki jest najlepszym sposobem na zminimalizowanie błędu próbkowania.
błąd standardowy vs odchylenie standardowe
błąd standardowy i odchylenie standardowe są miarami zmienności:
- odchylenie standardowe opisuje zmienność w obrębie jednej próbki.
- standardowy błąd szacuje zmienność w wielu próbkach populacji.


odchylenie standardowe jest statystyką opisową, którą można obliczyć na podstawie danych próbki. Natomiast błąd standardowy jest statystyką wnioskującą, którą można jedynie oszacować (o ile nie jest znany rzeczywisty parametr populacji).
odchylenie standardowe wyników matematycznych wynosi 180. Liczba ta odzwierciedla średnio, jak bardzo każdy wynik różni się od średniej z próby 550.
standardowy błąd wyników matematycznych, z drugiej strony, mówi, jak bardzo średnia z próby 550 różni się od innych średnich z próby, w próbkach o jednakowej wielkości, w populacji wszystkich uczestników testu w regionie.
wzór błędu standardowego
błąd standardowy średniej oblicza się przy użyciu odchylenia standardowego i wielkości próby.
ze wzoru zobaczysz, że rozmiar próbki jest odwrotnie proporcjonalny do błędu standardowego. Oznacza to, że im większa próbka, tym mniejszy błąd standardowy, ponieważ statystyka próbki będzie bliżej zbliżenia się do parametru populacji.
stosuje się różne wzory w zależności od tego, czy znane jest odchylenie standardowe populacji. Formuły te działają dla próbek z więcej niż 20 elementami (n > 20).
gdy parametry populacji są znane
gdy odchylenie standardowe populacji jest znane, możesz użyć go w poniższym wzorze do dokładnego obliczenia błędu standardowego.
| wzór | Wyjaśnienie |
|---|---|
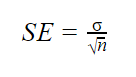 |
|
gdy parametry populacji są nieznane
gdy odchylenie standardowe populacji jest nieznane, można użyć poniższego wzoru tylko do oszacowania błędu standardowego. Wzór ten przyjmuje odchylenie standardowe próbki jako oszacowanie punktowe dla odchylenia standardowego populacji.
| wzór | Wyjaśnienie |
|---|---|
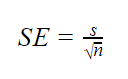 |
|
najpierw znajdź pierwiastek kwadratowy wielkości próbki (n).
| wzór | Obliczanie |
|---|---|
| √n | N = 200
√N = √200 = 14.1 |
następnie podziel odchylenie standardowe próbki przez liczbę znalezioną w kroku pierwszym.
| wzór | Obliczanie |
|---|---|
| SE = s ÷ √n | s = 180
√n = 14.1 s ÷ √N = 180 ÷ 14.1 = 12.8 |
standardowy błąd matematycznych wyników SAT wynosi 12,8.
Jak zgłosić błąd standardowy?
możesz zgłosić błąd standardowy obok średniej lub w przedziale ufności, aby zakomunikować niepewność wokół średniej.
najlepszym sposobem zgłoszenia błędu standardowego jest przedział ufności, ponieważ czytelnicy nie będą musieli wykonywać żadnej dodatkowej matematyki, aby wymyślić znaczący przedział.
przedział ufności to zakres wartości, w których nieznany parametr populacji powinien leżeć przez większość czasu, jeśli chcesz powtórzyć badanie z nowymi próbkami losowymi.
przy 95% poziomie ufności, 95% wszystkich średnich próbek będzie leżeć w przedziale ufności ± 1,96 błędów standardowych średniej próby.
w oparciu o losowe pobieranie próbek szacuje się, że rzeczywisty parametr populacji mieści się w tym zakresie z 95% ufnością.
dla normalnie rozmieszczonych cech, takich jak wyniki SAT, 95% wszystkich środków z próby mieści się w przybliżeniu w 4 standardowych błędach średniej z próby.
| wzór przedziału ufności | |
|---|---|
|
CI = x ± (1,96 × SE) x = średnia próbki = 550 |
|
| dolna granica | górna granica |
|
x – (1.96 × SE) 550 − (1.96 × 12.8) = 525 |
x + (1,96 × SE) 550 + (1.96 × 12.8) = 575 |
przy losowym pobieraniu próbek 95% CI mówi, że istnieje prawdopodobieństwo 0,95, że średnia liczba ludności wynosi między 525 a 575.
inne standardowe błędy
oprócz standardowego błędu średniej (i innych statystyk), istnieją dwa inne standardowe błędy, które możesz napotkać: standardowy błąd oszacowania i standardowy błąd pomiaru.
standardowy błąd oszacowania jest związany z analizą regresji. Odzwierciedla to zmienność wokół szacowanej linii regresji i dokładność modelu regresji. Korzystając ze standardowego błędu oszacowania, można skonstruować przedział ufności dla prawdziwego współczynnika regresji.
standardowy błąd pomiaru dotyczy wiarygodności pomiaru. Wskazuje, jak zmienny jest błąd pomiaru testu i jest często zgłaszany w standardowych testach. Standardowy błąd pomiaru może być użyty do utworzenia przedziału ufności dla prawdziwego wyniku elementu lub jednostki.
Często zadawane pytania dotyczące błędu standardowego
standardowy błąd średniej, lub po prostu standardowy błąd, wskazuje, jak różna jest średnia populacji od średniej próby. Informuje o tym, jak bardzo średnia z próby zmieniłaby się, gdybyś powtórzył badanie z użyciem nowych próbek z jednej populacji.
błąd standardowy i odchylenie standardowe są miarami zmienności. Odchylenie standardowe odzwierciedla zmienność w próbce, podczas gdy błąd standardowy szacuje zmienność w próbkach populacji.
korzystając ze statystyk opisowych i wnioskowych, możesz dokonać dwóch rodzajów szacunków dotyczących populacji: szacunków punktowych i oszacowań interwałowych.
- Estymator punktowy to Estymator pojedynczej wartości parametru. Na przykład, średnia próby jest oszacowanie punktu średniej populacji.
- oszacowanie interwału daje zakres wartości, w których oczekuje się, że parametr będzie leżał. Przedział ufności jest najczęstszym rodzajem oszacowania przedziału.
oba rodzaje szacunków są ważne dla zebrania jasnego pojęcia, gdzie parametr może leżeć.
