평균의 표준 오차 또는 단순히 표준 오차는 모집단 평균이 표본 평균과 얼마나 다를 수 있는지를 나타냅니다. 단일 모집단 내에서 새 표본을 사용하여 연구를 반복할 경우 표본 평균이 얼마나 달라지는지 알려줍니다.
평균의 표준 오차는 가장 일반적으로 보고되는 표준 오차 유형입니다. 그러나 중앙값 또는 비율과 같은 다른 통계에 대한 표준 오류를 찾을 수도 있습니다. 표준 오차는 샘플링 오차의 일반적인 척도(모집단 모수와 표본 통계량 간의 차이)입니다.
표준 오류가 중요한 이유
통계에서 샘플의 데이터는 더 큰 집단을 이해하는 데 사용됩니다. 표준 오류는 표본 데이터가 전체 모집단을 얼마나 잘 나타내는지를 추정하는 데 도움이 되기 때문에 중요합니다.
샘플의 요소가 무작위로 선택되는 확률 샘플링을 사용하면 모집단을 대표 할 가능성이있는 데이터를 수집 할 수 있습니다. 그러나 확률 샘플이 있더라도 일부 샘플링 오류가 남아 있습니다. 그 이유는 표본이 평균 및 표준 편차와 같은 측정값 측면에서 오는 모집단과 완벽하게 일치하지 않기 때문입니다.
표준 오차를 계산하여 표본이 모집단의 대표성을 추정하고 유효한 결론을 내릴 수 있습니다.
높은 표준 오차는 표본 평균이 모집단 평균 주위에 널리 퍼져 있음을 보여줍니다. 표준 오차가 낮 으면 표본 평균이 모집단 평균 주위에 밀접하게 분포되어 있음을 알 수 있습니다.
표본 크기를 늘려 표준 오차를 줄일 수 있습니다. 큰 무작위 샘플을 사용하는 것이 샘플링 편향을 최소화하는 가장 좋은 방법입니다.
표준 오차 대 표준 편차
표준 오차와 표준 편차는 모두 가변성의 척도입니다:
- 표준 편차는 단일 표본 내의 변동성을 설명합니다.
- 표준 오차는 모집단의 여러 표본에 걸친 변동성을 추정합니다.


표준 편차는 샘플 데이터에서 계산할 수 있는 설명 통계량입니다. 대조적으로,표준 오차는 실제 모집단 매개 변수가 알려지지 않은 경우에만 추정 할 수있는 추론 통계입니다.
수학 점수의 표준 편차는 180 입니다. 이 숫자는 각 점수가 550 의 표본 평균 점수와 얼마나 다른지 평균을 반영합니다.
반면에 수학 점수의 표준 오차는 표본 평균 점수 550 이 지역의 모든 응시자 모집단에서 동일한 크기의 표본에서 다른 표본 평균 점수와 얼마나 다른지 알려줍니다.
표준 오차 공식
평균의 표준 오차는 표준 편차 및 표본 크기를 사용하여 계산됩니다.
수식에서 표본 크기가 표준 오차에 반비례하는 것을 볼 수 있습니다. 즉,표본 통계량이 모집단 모수에 근접하기 때문에 표본이 클수록 표준 오차가 작아집니다.
모집단 표준 편차가 알려져 있는지 여부에 따라 다른 공식이 사용됩니다. 이 수식은 20 개 이상의 요소가있는 샘플에 대해 작동합니다(엔>20).
모집단 매개 변수가 알려진 경우
모집단 표준 편차가 알려진 경우 아래 공식에서 표준 오차를 정확하게 계산할 수 있습니다.
| 공식 | 설명 |
|---|---|
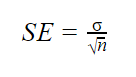 |
|
모집단 모수를 알 수 없는 경우
모집단 표준 편차를 알 수 없는 경우 아래 수식을 사용하여 표준 오차만 추정할 수 있습니다. 이 수식은 표본 표준 편차를 모집단 표준 편차에 대한 점 추정치로 사용합니다.
| 공식 | 설명 |
|---|---|
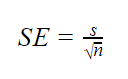 |
|
먼저 표본 크기의 제곱근을 찾습니다.
| 공식 | 계산 |
|---|---|
| √200,000,000,000,000,000,000,000,000,000,000,000,000,000= √200 = 14.1 |
그런 다음 샘플 표준 편차를 1 단계에서 찾은 숫자로 나눕니다.
| 공식 | 계산 |
|---|---|
| 14.1
14.1 14.1 15.1>15.1>15.1>15.1>15.1>15.1>15.1>15.1>15.1>15.1>15.1>15.1>= 180 ÷ 14.1 = 12.8 |
수학 토 점수의 표준 오류는 12.8 입니다.
표준 오류를 어떻게 보고해야 합니까?
표준 오차를 평균과 함께 또는 신뢰 구간에서 보고하여 평균에 대한 불확실성을 전달할 수 있습니다.
표준 오류를 보고하는 가장 좋은 방법은 신뢰 구간입니다.
신뢰 구간은 새로운 무작위 표본으로 연구를 반복하는 경우 알 수 없는 모집단 모수가 대부분의 시간에 속할 것으로 예상되는 값 범위입니다.
95%신뢰 수준으로,모든 샘플 평균의 95%는 샘플 평균의 1.96 표준 오차의 신뢰 구간 내에 있을 것으로 예상됩니다.
무작위 샘플링을 기반으로 실제 모집단 매개 변수도이 범위 내에 95%신뢰가있는 것으로 추정됩니다.
토 점수와 같은 정규 분포 특성의 경우 모든 샘플 평균의 95%가 샘플 평균의 약 4 가지 표준 오차에 속합니다.
| 신뢰 구간 공식 | |
|---|---|
|
예를 들어,샘플의 평균값은 1.96 이고,샘플의 평균값은 1.96 이고,샘플의 평균값은 1.96 이고,샘플의 평균값은 1.96 이고,샘플의 평균값은 1.96 이고,샘플의 평균값은 1.96 이고,샘플의 평균값은 1.96 입니다.= 12.8 |
|
| 하한 | 상한 |
|
엑스-(1.96×SE) 550 − (1.96 × 12.8) = 525 |
x+(1.96×SE) 550 + (1.96 × 12.8) = 575 |
무작위 샘플링,95%CI 알 수 있 0.95 확률이 평균 인구는 수학 SAT 점수는 사 525 및 575.
기타 표준 오차
평균(및 기타 통계)의 표준 오차 외에도 예상 표준 오차와 측정 표준 오차라는 두 가지 다른 표준 오차가 있습니다.
추정치의 표준 오차는 회귀 분석과 관련이 있습니다. 이는 추정 회귀선 주변의 변동성과 회귀 모델의 정확도를 반영합니다. 추정치의 표준 오차를 사용하여 실제 회귀 계수에 대한 신뢰 구간을 작성할 수 있습니다.
측정의 표준 오차는 측정의 신뢰성에 관한 것입니다. 그것은 테스트의 측정 오차가 얼마나 가변적인지 나타내며 표준화 된 테스트에서 종종 보고됩니다. 측정의 표준 오차는 요소 또는 개인의 실제 점수에 대한 신뢰 구간을 만드는 데 사용할 수 있습니다.
표준 오류에 대한 자주 묻는 질문
평균의 표준 오차 또는 단순히 표준 오차는 모집단 평균이 표본 평균과 얼마나 다를 수 있는지를 나타냅니다. 단일 모집단 내에서 새 표본을 사용하여 연구를 반복할 경우 표본 평균이 얼마나 달라지는지 알려줍니다.
표준 오차 및 표준 편차는 모두 변동성의 척도입니다. 표준 편차는 표본 내의 변동성을 반영하는 반면 표준 오차는 모집단의 표본 간 변동성을 추정합니다.
설명 및 추론 통계를 사용하여 모집단에 대한 두 가지 유형의 추정치(점 추정치 및 구간 추정치)를 만들 수 있습니다.
- 포인트 추정치는 모수의 단일 값 추정치입니다. 예를 들어 표본 평균은 모집단 평균의 점 추정치입니다.
- 구간 추정치는 매개변수가 있을 것으로 예상되는 값의 범위를 제공합니다. 신뢰 구간은 가장 일반적인 구간 추정 유형입니다.
두 가지 유형의 추정치는 매개 변수가 어디에 있을지에 대한 명확한 아이디어를 수집하는 데 중요합니다.
