Wie berechnet man den P-Wert in Excel?

Inhalt

1. 1. Was ist der P-Wert?
   2. Warum brauchen wir den P-Wert?
   3. Wo verwenden wir den P-Wert im wirklichen Leben?
      • Marketing
      • Wahrscheinlichkeit
   4. Wie berechnet man den P-Wert in Excel?
   5. SCHLUSSWORTE

Was ist der P-Wert?

Der P-Wert ist ein statistischer Begriff, der Ihnen hilft, die Wahrscheinlichkeit der Stichprobenvariation zu bestimmen, wenn die von Ihnen verwendete Hypothese wahr ist. Es sagt uns einfach, wie hoch die Chancen sind, diese Ergebnisse zu erhalten, wenn unsere Nullhypothese wahr ist.

• Eine Nullhypothese ist eine Hypothese, die behauptet, dass die Ergebnisse, die wir erhalten, durch reines Glück verursacht werden.
• Eine alternative Hypothese behauptet, dass die Ergebnisse, die wir erhalten, kein Glück sind, sondern dass es äußere Elemente gibt, die unsere Ergebnisse beeinflussen.

Es ist ein sehr wichtiger und häufig verwendeter statistischer Begriff und kann leicht in Datenanalyseprogrammen wie Microsoft Excel berechnet werden. In diesem Artikel erfahren Sie, wie wir es verwenden, wo wir es verwenden und wie wir es in Excel auf verschiedene Arten berechnen können.

Fangen wir an!

Warum brauchen wir den P-Wert?

Bei der Forschung mit großen Populationen müssen Sie die Statistiken für jeden Einzelnen berechnen. Aber selbst in einem solchen Fall können Sie nicht sicher sein, ob etwas zufällig oder einfach nur durch Glück passiert ist, da es unmöglich ist, alles zu beobachten. Hier kommen die Statistiken ins Spiel.

Statistische Berechnungen können Ihnen keine absolute Wahrheit geben, aber sie werden Ihnen helfen, eine gute Vorstellung von Ihren Forschungen zu haben.

Mit dem P-Wert können wir die Hypothese zu unserem Thema testen. Wir können die mathematischen Ergebnisse mit diesen Hypothesen vergleichen und unseren Weg überdenken, ohne viel Zeit in die Forschung zu investieren.

Wo verwenden wir den P-Wert im wirklichen Leben?

Wir verwenden den Wahrscheinlichkeitswert, um eine Hypothese zu testen. Es kann um Forschung oder eine einfache Wette gehen, die wir mit unserem Freund gemacht haben.

Es ist einfacher, es mit Beispielen zu verstehen.

Marketing:

Angenommen, Sie arbeiten im Marketingbereich und Ihr aktuelles Projekt befasst sich mit Online-Werbung.

Sie haben ein Video für soziale Medien produziert und Sie haben die Informationen dafür, dass Benutzer es übersprungen oder lange angesehen haben.

Die übliche Wiedergabezeit des Videos beträgt beispielsweise 20 Sekunden. Der Mittelwert beträgt 20 Sekunden. Und Sie haben die Entscheidung getroffen, das Video mit einem Stück fröhlicherer Musik zu bearbeiten.

Wie erkennen Sie nun, ob es funktioniert hat? An dieser Stelle verwenden wir Signifikanzstatistiken.

Erstellen Sie zunächst eine Nullhypothese:

Eine Nullhypothese behauptet, dass es keine Korrelation zwischen dem, was Sie investieren, und den Ergebnissen gibt, die Sie erhalten. Es hat keinen Einfluss auf die Ergebnisse.

In diesem Beispiel lautet die Nullhypothese: „Es besteht keine Beziehung zwischen den Änderungen, die Sie auf die Wiedergabezeit anwenden.“

Dann die alternative Hypothese:

Die alternative Hypothese legt nahe, dass das Ändern der Musik tatsächlich funktioniert hat und die Leute den Werbespot jetzt länger als 20 Sekunden sehen. Mathematisch sagt die Alternativhypothese:

„Der Mittelwert ist jetzt größer als 20 Sekunden.“

Berechnen Sie das Signifikanzniveau:

Jetzt müssen wir eine Grenzschwelle setzen, um zu berechnen, ob wir erfolgreich sind oder nicht. Dies wird als Signifikanzniveau bezeichnet und zusätzlich als Alpha-Wert bezeichnet. Es kann jeder Prozentsatz sein, den Sie möchten, es liegt absolut bei Ihnen.

Aber in diesem Beispiel wird es 0,05 sein.

Um nun mit Sicherheit zu berechnen, sollten wir immer alle Daten der Uhrzeit haben. In Bezug auf Ihre Zeit und Quellen sollten Sie jedoch eine Stichprobe aus der Bevölkerung entnehmen:

1. Sie haben eine Stichprobe von 100 Personen genommen.
2. Diese 100 Personen haben 25 Sekunden Zeit für den Werbespot.
3. Es bedeutet, dass der Mittelwert der Stichprobe 25 ist.

Dies ist eine sehr einfache Version der Berechnung. Die Standardabweichung der Stichprobe wird jedoch normalerweise in dieser Skala berechnet, wenn Sie die Standardabweichung der gesamten Grundgesamtheit nicht kennen.

Sie können die Werte verwenden, die Sie für die Stichprobe berechnet haben, da sie nahe an den Grundgesamtheitswerten liegen. Der Mittelwert der Stichprobe liegt nahe am Mittelwert der Grundgesamtheit.

P-Wert berechnen:

Der p-Wert zeigt uns, ob wir die Nullhypothese ablehnen können oder nicht. Die Wahrscheinlichkeit, dass der Stichprobenmittelwert unter Berücksichtigung der Nullhypothese größer oder gleich 25 Minuten ist, ist wahr.

Es gibt zwei Situationen, die passieren können.

1. Wenn der p-Wert kleiner als das Alpha ist, können Sie die Nullhypothese ablehnen. Sie haben den statistischen Beweis, dass die Alternativhypothese wahr ist.
2. Wenn der p-Wert jedoch größer oder gleich dem Alpha ist, können Sie die Nullhypothese nicht ablehnen. Es bedeutet nicht, dass die Nullhypothese sicherlich wahr ist, aber es kann auch nicht vermieden werden.

Lassen Sie uns an einem anderen Beispiel arbeiten.

Dein Freund und du haben Münze in die Luft geworfen: Wenn es Schwänze sind, verlierst du 5 Dollar und wenn es Köpfe gibt, gewinnst du 5 Dollar.

• Ihr Freund wirft die Münze einmal: Es kommt als Schwänze. Es ist okay, es gibt eine 50% Chance, dass es als Schwänze kommen wird. Nun gehen Sie davon aus, dass die Wahrscheinlichkeit 0,5 beträgt, weil Sie glauben, dass es sich um eine faire Münze handelt. Dies ist Ihre Nullhypothese.

• Zweitens: Es ist Schwänze. Sie haben weitere 5 Dollar verloren, aber es ist in Ordnung, weil es immer noch eine gute Chance auf zwei Schwänze hintereinander gibt. Der p-Wert ist 0,25 und es ist immer noch ein faires Verhältnis.
• Drittens: Es ist wieder Tails. Die Chance, dreimal hintereinander zu gewinnen, beträgt 0,12. Es ist nicht niedrig, daher gibt es nicht genügend Beweise dafür, dass die Nullhypothese nicht korrekt ist. Aber Sie beginnen zu denken, dass Ihre alternative Hypothese richtig sein könnte.
• Viertens: Es stellt sich wieder heraus, dass Sie sehen werden, wie die Chancen wirklich niedrig werden. Es kann ein wundersamer Zufall sein, aber es gibt immer noch eine 0,6-Chance und es gibt immer noch nicht genügend Beweise, um die alternative Hypothese zu stützen, die besagt, dass die Münze schwierig ist. Und du wartest auf den fünften Flip.
• Fünftens: Es sind Schwänze. Die Chance, dass sich eine Münze fünfmal hintereinander als Schwanz herausstellt, beträgt 0,3, was sehr niedrig ist. Dies ist der Punkt, an dem Sie die Nullhypothese ablehnen können, da es nicht mehr genügend Beweise gibt, um sie zu stützen.

Sie bitten Ihren Freund, die Münze zu sehen, und wenn Sie sie halten, stellen Sie fest, dass sie zwei Schwänze hat und eine knifflige Münze ist.

Was hat dazu geführt, dass wir den Glauben an unsere Nullhypothese verloren haben?

In einem fairen Spiel, in dem Münzen geworfen werden, beträgt die Chance, einen Kopf oder einen Zahl zu erhalten, 50%. Dies ist eine Situation, in der wir glauben, dass die Münze fair ist, aber da der p-Wert sinkt, wird auch unser Vertrauen in diese Hypothese geschwächt.

Es besteht kaum eine Chance, zufällige Schwänze zu haben, wenn der p-Wert unter 0,05 fällt. Wenn Sie diesen statistischen Begriff also auf Themen wie Krebsforschung oder Auswirkungen des Klimawandels anwenden, gewinnt er an Bedeutung.

Hinweis: Es gibt keinen bestimmten Grund, warum wir 0,05 p-Wert für die Standardberechnung verwenden. Der Ersteller der Formel entschied, dass dies eine gute Zahl für die Berechnung war, und die Standardberechnungen bleiben dabei. 0,05 bedeutet 5% bei 100 Personen, was in die normale Kurve fällt. Dies ist einer der Gründe, warum es häufig verwendet wird. Wenn Sie es während der Berechnung selbst ändern möchten, können Sie dies tun.

Wie berechnet man den P-Wert in Excel?

Es gibt mehrere Möglichkeiten, den p-Wert in Microsoft Excel zu berechnen. Sie können Formeln eingeben oder das Analyse-ToolPak verwenden. Dieser Artikel enthält, wie es in beide Richtungen zu tun.

Verwendung klassischer Excel-Formeln:

Beginnen wir mit der klassischen Excel-Formel. Es gibt zwei Möglichkeiten, dies zu tun TDIST Formel und T-Test Formel.

1.1) TDIST-Formel

Zunächst benötigen Sie einen Datensatz, um einen p-Wert zu berechnen.

• Angenommen, Sie sind Lehrer und möchten vergleichen, was Ihre Schüler in Ihrer letzten Prüfung erzielt haben und was Sie aufgrund ihrer vorherigen Prüfungen erwartet haben.
• Sie haben die Ergebnisse 25, 46, 34, 27, 35, 43, 40, 44, 21 und 39 für Ihre letzte Prüfung.
• Jetzt für die Berechnung benötigen Sie einen anderen Schwanz, dies ist die Punktzahl, die Sie basierend auf früheren Tests erwartet haben: 23, 44, 32, 20, 46, 37, 35, 42, 33, und 35

Um nun die p-Wert-Formel in Excel zu verwenden, sollten Sie vorher einige Dinge berechnen:

Pearson-Koeffizient (r): Es ist ein statistischer Begriff, der die lineare Korrelation zwischen zwei Daten misst. Sie müssen den mathematischen Aspekt nicht kennen, um den p-Wert zu berechnen. Sie werden die einfache Formel dafür in den nächsten Absätzen sehen.

Population (n): n ist die Gesamtzahl der Personen in Ihrem Datensatz.

T Statistik: Es ist das Verhältnis der Abweichung des geschätzten Wertes von seinem angenommenen Wert zu seinem Standardfehler.

Freiheitsgrad: Es ist die Anzahl der Personen im Datensatz minus zwei.

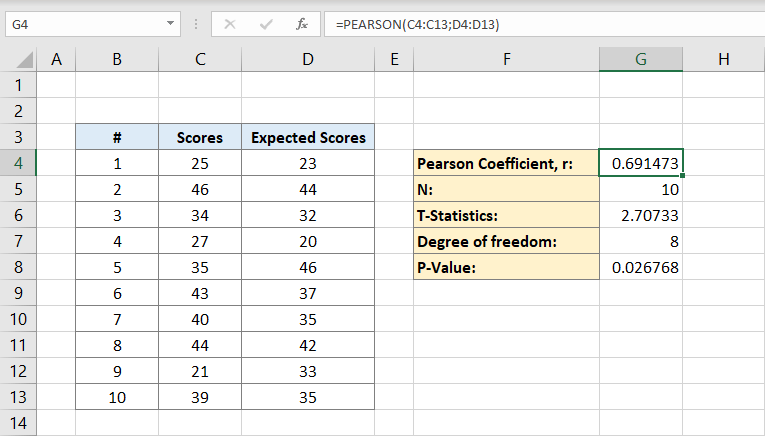
Nun wird der Pearson-Koeffizient in diesem Beispiel auf F4 geschrieben. Nachdem Sie darauf geklickt haben, geben Sie die Formel ein:

C Spalten sind für die Noten und D Spalten sind für die erwarteten Noten. Der Pearson-Koeffizient beträgt in diesem Beispiel 0,691473.

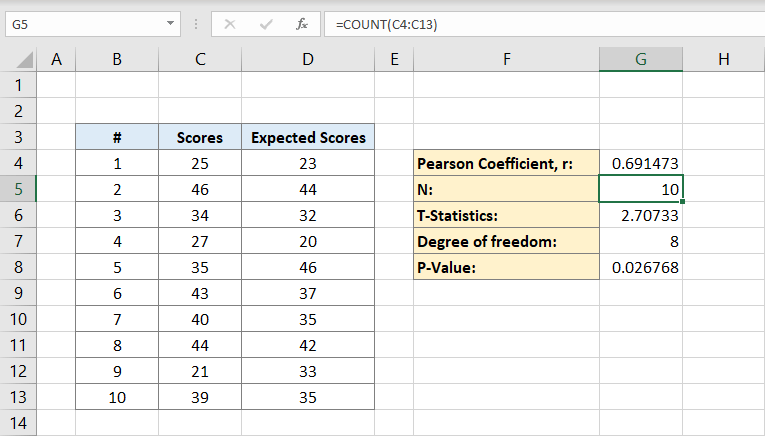
Als nächstes geben Sie die Anzahl der Personen im Datensatz ein. Wenn Sie sicher wissen, wie viele Personen Sie haben, können Sie es manuell eingeben, aber wenn Sie dies nicht tun, können Sie die Formel verwenden:

Warum enthält die Formel nur eine C-Spalte?

Dies liegt daran, dass wir nur die Personen in einem Datensatz benötigen, um zu berechnen, dass eine Spalte ausreicht. Die Zelle G5 enthält nun die Zahl 10. Das ist unsere Bevölkerung.

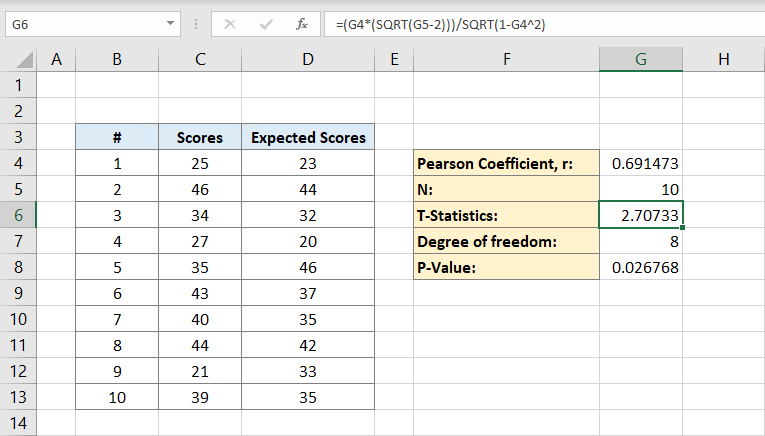
Jetzt, da Sie sowohl den Pearson-Koeffizienten als auch die Population haben, können Sie T-Statistiken berechnen. Die mathematische Formel für die T-Statistik ist der Pearson-Koeffizient (r) mal Vorzeichen Quadratwurzel der Bevölkerung (n) minus 2 geteilt durch die Quadratwurzel von 1 minus Pearson-Koeffizient im Quadrat:

Die Zelle G6 enthält das Ergebnis 2,70733. Dies ist unsere T-Statistik.

Danach berechnen Sie den Freiheitsgrad. Sie geben ein:

In die Zelle G7. Dies ist der Grad der Freiheit. Es wird um 8 Uhr sein.

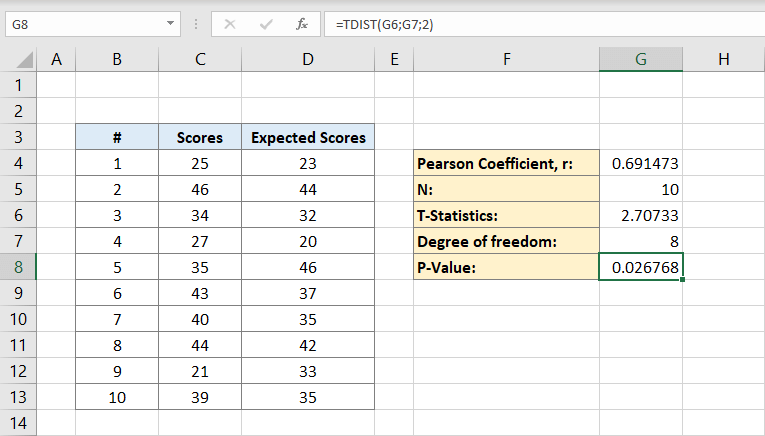
Jetzt haben Sie alles, was Sie brauchen, um den P-Wert zu berechnen. Die Zelle G8 enthält die Formel dafür. Das heißt:

Oder

Das Ergebnis ist 0,026768. Dies ist der p-Wert für den Datensatz.

1.2. T-Test-Formel

Die zweite Möglichkeit, den p-Wert mit Excel-Formeln zu bestimmen, ist die Verwendung der T-Test-Formel. Es ist ein bisschen ähnlich wie das vorherige Beispiel, aber kürzer.

• Angenommen, der Datensatz ist derselbe, Sie haben die Ergebnisse 25, 46, 34, 27, 35,43, 40, 44, 21, 39 für Ihre letzte Prüfung.
• Erwartete Ergebnisse sind 23, 44, 32, 20, 46, 37, 35, 42, 33, 35.
• Sie werden eine dritte Spalte für die Differenz zwischen dem erwarteten und dem tatsächlichen Ergebnis hinzufügen. In der Spalte Differenz 2, 2, 2, 7, 11, 6, 5, 2, 12, 4 wird von E4 bis E13 geschrieben.

Geben Sie nun T-Test in die Zelle E8 ein. Sie werden die T-Test-Formel in die leere Zelle daneben schreiben. Das heißt:

Und diese Formel gibt Ihnen den p-Wert direkt.

Bestimmen Sie den P-Wert mit dem Excel-Tool Pak

Excel Pak ist ein Paket, mit dem Sie verschiedene statistische Messungen automatisch berechnen können, sodass es einfach und sehr praktisch ist. Es ist auch einfach zu installieren.

Schritt 1: Gehen Sie zu Einstellungen. Unten in der linken Ecke befindet sich die Schaltfläche „Add-Ins“. Suchen Sie die Option „Analysis Tool Pak“, klicken Sie darauf und dann auf die Schaltfläche „Los“ am unteren Rand des Fensters.

Schritt 2: Aktivieren Sie das Add-In, indem Sie auf das Häkchen-Symbol daneben und nach dem OK-Button in der rechten Spalte klicken.

Schritt 3: Wenn Sie es richtig aktiviert haben, wird im oberen Menü Ihres Arbeitsblatts auf der rechten Seite die Schaltfläche „Datenanalyse“ angezeigt.

Schritt 4: Klicken Sie Auf die „Daten analyse“ taste und wählen sie die „t-Test: Gepaart Zwei Probe für Bedeutet“ option. Klicken Sie danach auf OK. Es erscheint ein neues Fenster.

Schritt 5: Es werden die Eingaben in der ersten Zeile des Fensters abgefragt. Geben Sie C4: C13 in das Feld „Variabler 1-Bereich“ ein. Sie geben D4: D13 in das Feld „Variabler 2-Bereich“ ein. Belassen Sie das Alpha-Feld mit seinem Standardwert.

Schritt 6: In der zweiten Zeile des Fensters können Sie auswählen, wo Ihre Ergebnisse überwacht werden sollen. Es kann ein neues Arbeitsblatt oder leere Zellen sein. Wenn Sie das Ergebnis in einer Zelle haben möchten, stellen Sie sicher, dass Sie die Spalte und die Zeile sperren. Klicken Sie danach auf die Schaltfläche OK.

Tipp: Verwenden Sie das Dollarzeichen vor dem Buchstaben und der Zahl, um die Spalte und Zeile zu sperren. Wenn Sie beispielsweise eine 2-Zelle sperren möchten, geben Sie $ A $ 2 ein.

Schritt 7: Das Excel berechnet den Mittelwert, die Varianz, die Beobachtungen, die Pearson-Korrelation, die hypothetische mittlere Differenz, die t-Statistik, den p-Wert und mehr.

SCHLUSSWORTE

Der P-Wert ist einfach zu berechnen und in vielen verschiedenen Situationen anzupassen. Es hilft Ihnen, die Informationen zu erhalten, die Sie benötigen, ohne viel Zeit oder Mühe darauf zu verwenden. Es ist noch einfacher zu berechnen, wenn Sie statistische Analyseprogramme wie Microsoft Excel verwenden, die mit den richtigen Tools und Formeln geliefert werden. Lassen Sie uns eine Sammlung statistischer Vorlagen überprüfen und statistische Vorlagen herunterladen, um Ihre Arbeit zu erleichtern!

Verwandte Messwerte:

• Wie berechne ich das Konfidenzintervall in Excel?
• Kann Excel Daten analysieren?