Der Standardfehler des Mittelwerts oder einfach Standardfehler gibt an, wie unterschiedlich der Mittelwert der Grundgesamtheit wahrscheinlich von einem Stichprobenmittelwert ist. Hier erfahren Sie, wie stark der Stichprobenmittelwert variieren würde, wenn Sie eine Studie mit neuen Stichproben aus einer einzelnen Population wiederholen würden.
Der Standardfehler des Mittelwerts (SE oder SEM) ist die am häufigsten gemeldete Art von Standardfehler. Sie können den Standardfehler aber auch für andere Statistiken wie Mediane oder Proportionen finden. Der Standardfehler ist ein gängiges Maß für den Stichprobenfehler — die Differenz zwischen einem Populationsparameter und einer Stichprobenstatistik.
Warum Standardfehler wichtig sind
In der Statistik werden Daten aus Stichproben verwendet, um größere Populationen zu verstehen. Standardfehler sind wichtig, da Sie damit abschätzen können, wie gut Ihre Stichprobendaten die gesamte Grundgesamtheit darstellen.
Mit Wahrscheinlichkeitsstichproben, bei denen Elemente einer Stichprobe zufällig ausgewählt werden, können Sie Daten erfassen, die wahrscheinlich repräsentativ für die Grundgesamtheit sind. Selbst bei Wahrscheinlichkeitsstichproben bleibt jedoch ein gewisser Stichprobenfehler bestehen. Das liegt daran, dass eine Stichprobe in Bezug auf Maße wie Mittelwerte und Standardabweichungen niemals perfekt mit der Grundgesamtheit übereinstimmt, aus der sie stammt.
Durch die Berechnung des Standardfehlers können Sie abschätzen, wie repräsentativ Ihre Stichprobe für Ihre Grundgesamtheit ist, und gültige Schlussfolgerungen ziehen.
Ein hoher Standardfehler zeigt, dass die Mittelwerte der Stichprobe weit über den Mittelwert der Grundgesamtheit verteilt sind – Ihre Stichprobe entspricht möglicherweise nicht genau der Grundgesamtheit. Ein niedriger Standardfehler zeigt, dass die Stichprobenmittelwerte eng um den Mittelwert der Grundgesamtheit verteilt sind – Ihre Stichprobe ist repräsentativ für Ihre Grundgesamtheit.
Sie können den Standardfehler verringern, indem Sie die Stichprobengröße erhöhen. Die Verwendung einer großen Zufallsstichprobe ist der beste Weg, um den Sampling-Bias zu minimieren.
Standardfehler vs Standardabweichung
Standardfehler und Standardabweichung sind beide Maße der Variabilität:
- Die Standardabweichung beschreibt die Variabilität innerhalb einer einzelnen Stichprobe.
- Der Standardfehler schätzt die Variabilität über mehrere Stichproben einer Population hinweg.


Die Standardabweichung ist eine deskriptive Statistik, die aus Beispieldaten berechnet werden kann. Im Gegensatz dazu ist der Standardfehler eine Inferenzstatistik, die nur geschätzt werden kann (es sei denn, der reale Populationsparameter ist bekannt).
Die Standardabweichung der mathematischen Werte beträgt 180. Diese Zahl spiegelt im Durchschnitt wider, wie sehr sich jede Punktzahl von der mittleren Punktzahl der Stichprobe von 550 unterscheidet.
Der Standardfehler der mathematischen Punktzahlen hingegen gibt an, wie sehr sich der mittlere Wert der Stichprobe von 550 von anderen mittleren Werten der Stichprobe in Stichproben gleicher Größe in der Grundgesamtheit aller Testteilnehmer in der Region unterscheidet.
Standardfehlerformel
Der Standardfehler des Mittelwerts wird unter Verwendung der Standardabweichung und des Stichprobenumfangs berechnet.
Aus der Formel sehen Sie, dass der Stichprobenumfang umgekehrt proportional zum Standardfehler ist. Dies bedeutet, dass der Standardfehler umso kleiner ist, je größer die Stichprobe ist, da die Stichprobenstatistik näher an den Populationsparameter heranrückt.
Je nachdem, ob die Standardabweichung der Grundgesamtheit bekannt ist, werden unterschiedliche Formeln verwendet. Diese Formeln funktionieren für Proben mit mehr als 20 Elementen (n > 20).
Wenn Populationsparameter bekannt sind
Wenn die Populationsstandardabweichung bekannt ist, können Sie sie in der folgenden Formel verwenden, um den Standardfehler genau zu berechnen.
| Formel | Erklärung |
|---|---|
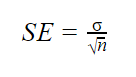 |
|
Wenn die Parameter der Grundgesamtheit unbekannt sind
Wenn die Standardabweichung der Grundgesamtheit unbekannt ist, können Sie die folgende Formel verwenden, um nur den Standardfehler zu schätzen. Diese Formel verwendet die Standardabweichung der Stichprobe als Punktschätzung für die Standardabweichung der Grundgesamtheit.
| Formel | Erklärung |
|---|---|
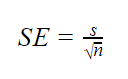 |
|
Ermitteln Sie zunächst die Quadratwurzel Ihrer Stichprobengröße (n).
| Formel | Berechnung |
|---|---|
| √ n | n = 200
√n = √200 = 14.1 |
Teilen Sie als Nächstes die Standardabweichung der Stichprobe durch die Zahl, die Sie in Schritt eins gefunden haben.
| Formel | Berechnung |
|---|---|
| SE = s ÷ √n | s = 180
√n = 14,1 s ÷ √n = 180 ÷ 14.1 = 12.8 |
Der Standardfehler von Math SAT Scores ist 12.8.
Wie sollten Sie den Standardfehler melden?
Sie können den Standardfehler neben dem Mittelwert oder in einem Konfidenzintervall melden, um die Unsicherheit um den Mittelwert zu kommunizieren.
Der beste Weg, den Standardfehler zu melden, ist in einem Konfidenzintervall, da die Leser keine zusätzlichen Berechnungen durchführen müssen, um ein aussagekräftiges Intervall zu ermitteln.
Ein Konfidenzintervall ist ein Wertebereich, in dem erwartet wird, dass ein unbekannter Populationsparameter die meiste Zeit liegt, wenn Sie Ihre Studie mit neuen Zufallsstichproben wiederholen.
Bei einem Konfidenzniveau von 95% wird erwartet, dass 95% aller Stichprobenmittelwerte innerhalb eines Konfidenzintervalls von ± 1,96 Standardfehlern des Stichprobenmittelwerts liegen.
Basierend auf einer Zufallsstichprobe wird auch geschätzt, dass der wahre Populationsparameter mit 95% iger Sicherheit in diesem Bereich liegt.
Für ein normalverteiltes Merkmal, wie SAT-Scores, fallen 95% aller Stichprobenmittelwerte innerhalb von ungefähr 4 Standardfehlern des Stichprobenmittelwerts.
| Konfidenzintervall Formel | |
|---|---|
|
CI = x ± (1,96 × SE) x = Mittelwert der Stichprobe = 550 |
|
| Untere Grenze | Obere Grenze |
|
x – (1.96 × SO) 550 − (1.96 × 12.8) = 525 |
x + (1,96 × SE) 550 + (1.96 × 12.8) = 575 |
Bei einer Zufallsstichprobe zeigt ein 95% -KI an, dass eine Wahrscheinlichkeit von 0,95 besteht, dass der mittlere mathematische SAT-Score der Grundgesamtheit zwischen 525 und 575 liegt.
Andere Standardfehler
Neben dem Standardfehler des Mittelwerts (und anderer Statistiken) gibt es zwei weitere Standardfehler, auf die Sie möglicherweise stoßen: den Standardfehler der Schätzung und den Standardfehler der Messung.
Der Standardfehler der Schätzung bezieht sich auf die Regressionsanalyse. Dies spiegelt die Variabilität um die geschätzte Regressionslinie und die Genauigkeit des Regressionsmodells wider. Mit dem Standardfehler der Schätzung können Sie ein Konfidenzintervall für den wahren Regressionskoeffizienten erstellen.
Beim Standardmessfehler geht es um die Zuverlässigkeit eines Maßes. Es gibt an, wie variabel der Messfehler eines Tests ist, und es wird oft in standardisierten Tests gemeldet. Der Standardmessfehler kann verwendet werden, um ein Konfidenzintervall für die wahre Punktzahl eines Elements oder einer Person zu erstellen.
Häufig gestellte Fragen zum Standardfehler
Der Standardfehler des Mittelwerts oder einfach Standardfehler gibt an, wie unterschiedlich der Mittelwert der Grundgesamtheit wahrscheinlich von einem Mittelwert der Stichprobe ist. Hier erfahren Sie, wie stark der Stichprobenmittelwert variieren würde, wenn Sie eine Studie mit neuen Stichproben aus einer einzelnen Population wiederholen würden.
Standardfehler und Standardabweichung sind beide Maße der Variabilität. Die Standardabweichung spiegelt die Variabilität innerhalb einer Stichprobe wider, während der Standardfehler die Variabilität zwischen Stichproben einer Grundgesamtheit schätzt.
Mithilfe von deskriptiven und inferentiellen Statistiken können Sie zwei Arten von Schätzungen für die Grundgesamtheit vornehmen: Punktschätzungen und Intervallschätzungen.
- Eine Punktschätzung ist eine Einzelwertschätzung eines Parameters. Zum Beispiel ist ein Stichprobenmittelwert eine Punktschätzung eines Populationsmittels.
- Eine Intervallschätzung gibt Ihnen einen Wertebereich, in dem der Parameter voraussichtlich liegen wird. Ein Konfidenzintervall ist die häufigste Art der Intervallschätzung.
Beide Arten von Schätzungen sind wichtig, um eine klare Vorstellung davon zu erhalten, wo ein Parameter wahrscheinlich liegt.
