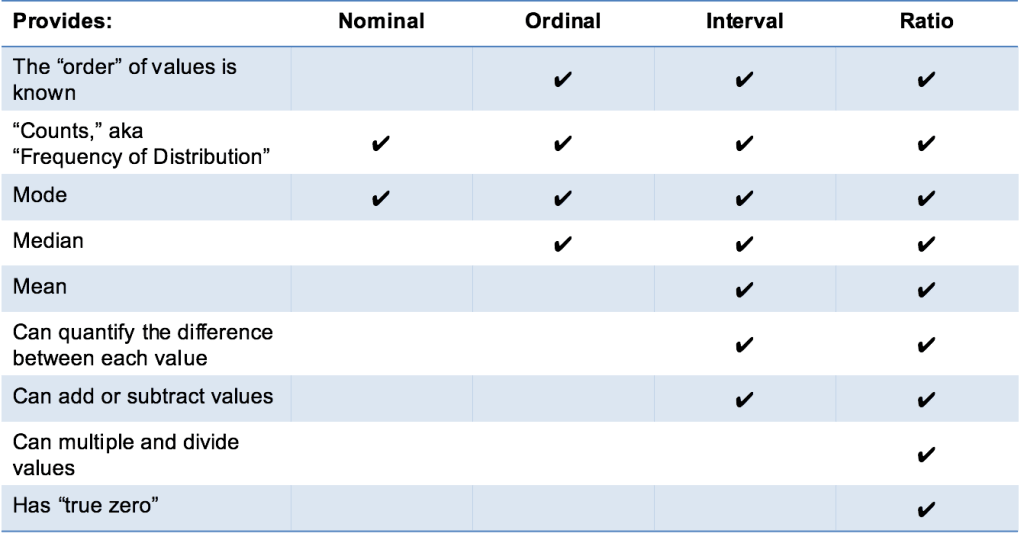
In der Statistik gibt es vier Datenmessskalen: nominal, ordinal, Intervall und Verhältnis. Dies sind einfache Möglichkeiten, verschiedene Datentypen zu unterkategorisieren (hier finden Sie eine Übersicht über statistische Datentypen) . Dieses Thema wird normalerweise im Rahmen der akademischen Lehre und seltener in der „realen Welt“ diskutiert.“ Wenn Sie dieses Konzept für einen Statistiktest auffrischen, danken Sie einem Psychologen namens Stanley Stevens für die Entwicklung dieser Begriffe.
Diese vier Datenmessskalen (Nominal, Ordinal, Intervall und Verhältnis) lassen sich am besten anhand eines Beispiels verstehen, wie Sie unten sehen werden.
Beginnen wir mit dem am einfachsten zu verstehenden. Nominalskalen werden zur Kennzeichnung von Variablen ohne quantitativen Wert verwendet. „Nominale“ Skalen könnten einfach als „Etiketten“ bezeichnet werden.“ Hier sind einige Beispiele, unten. Beachten Sie, dass sich alle diese Skalen gegenseitig ausschließen (keine Überlappung) und keine von ihnen numerische Bedeutung hat. Eine gute Möglichkeit, sich an all dies zu erinnern, ist, dass „nominal“ sehr nach „Name“ klingt und Nominalskalen wie „Namen“ oder Beschriftungen sind.
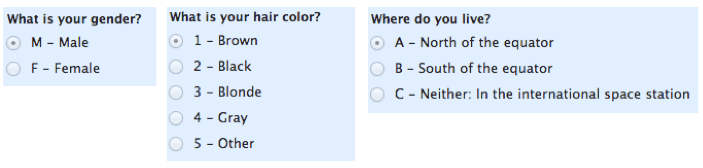
Hinweis: Ein Untertyp der Nennskala mit nur zwei Kategorien (z. B. männlich / weiblich) wird als „dichotom“ bezeichnet.“ Wenn Sie ein Student sind, können Sie das verwenden, um Ihren Lehrer zu beeindrucken.
Bonus Hinweis #2: Andere Untertypen von Nominaldaten sind „nominal mit Reihenfolge“ (wie „kalt, warm, heiß, sehr heiß“) und nominal ohne Reihenfolge (wie „männlich / weiblich“).
Ordinal
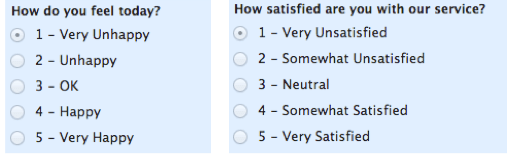
Bei Ordinalskalen ist die Reihenfolge der Werte wichtig und signifikant, aber die Unterschiede zwischen den einzelnen sind nicht wirklich bekannt. Schauen Sie sich das folgende Beispiel an. In jedem Fall wissen wir, dass eine # 4 besser ist als eine # 3 oder # 2, aber wir wissen nicht – und können nicht quantifizieren – wie viel besser es ist. Ist zum Beispiel der Unterschied zwischen „OK“ und „Unglücklich“ derselbe wie der Unterschied zwischen „Sehr glücklich“ und „Glücklich“?“ Wir können es nicht sagen.
Ordinalskalen sind typischerweise Maße für nicht numerische Konzepte wie Zufriedenheit, Glück, Unbehagen usw.
„Ordinal“ ist leicht zu merken, weil es wie „Ordnung“ klingt und das ist der Schlüssel, an den man sich mit „Ordinalskalen“ erinnern muss – es ist die Reihenfolge, die zählt, aber das ist alles, was man wirklich von diesen bekommt.
Fortgeschritten Hinweis: Der beste Weg, die zentrale Tendenz in einem Satz von Ordinaldaten zu bestimmen, ist die Verwendung des Modus oder Medians; Ein Purist wird Ihnen sagen, dass der Mittelwert nicht aus einem Ordinalsatz definiert werden kann.
Intervall
Intervallskalen sind numerische Skalen, bei denen wir sowohl die Reihenfolge als auch die genauen Unterschiede zwischen den Werten kennen. Das klassische Beispiel für eine Intervallskala ist die Celsius-Temperatur, da die Differenz zwischen den einzelnen Werten gleich ist. Zum Beispiel ist der Unterschied zwischen 60 und 50 Grad messbare 10 Grad, ebenso wie der Unterschied zwischen 80 und 70 Grad.
Intervallskalen sind nett, weil sich der Bereich der statistischen Analyse dieser Datensätze öffnet. Beispielsweise kann die zentrale Tendenz nach Modus, Median oder Mittelwert gemessen werden.
Wie die anderen können Sie sich die wichtigsten Punkte einer „Intervallskala“ ziemlich leicht merken. „Intervall“ selbst bedeutet „Raum dazwischen“, was wichtig ist – Intervallskalen sagen uns nicht nur über die Reihenfolge, sondern auch über den Wert zwischen den einzelnen Elementen.
Hier ist das Problem mit Intervallskalen: Sie haben keine „wahre Null“.“ Zum Beispiel gibt es keine „keine Temperatur“, zumindest nicht mit Celsius. Bei Intervallskalen bedeutet Null nicht das Fehlen eines Werts, sondern ist tatsächlich eine andere Zahl, die auf der Skala verwendet wird, z. B. 0 Grad Celsius. Negative Zahlen haben auch Bedeutung. Ohne eine echte Null ist es unmöglich, Verhältnisse zu berechnen. Mit Intervalldaten können wir addieren und subtrahieren, aber nicht multiplizieren oder dividieren.
Verwirrt? Ok, bedenken Sie Folgendes: 10 Grad C + 10 Grad C = 20 Grad C. Kein Problem dort. 20 Grad C sind jedoch nicht doppelt so heiß wie 10 Grad C, da es auf der Celsius-Skala keine „keine Temperatur“ gibt. Bei Umrechnung in Fahrenheit ist klar: 10C = 50F und 20C = 68F, was eindeutig nicht doppelt so heiß ist. Ich hoffe, das ergibt Sinn. Unterm Strich sind Intervallskalen großartig, aber wir können keine Verhältnisse berechnen, was uns zu unserer letzten Messskala bringt…

Verhältnis
Verhältnisskalen sind das ultimative Nirwana, wenn es um Datenmessskalen geht, weil sie uns über die Reihenfolge informieren, sie sagen uns den genauen Wert zwischen den Einheiten, UND sie haben auch einen absoluten Nullpunkt – was eine breite Palette von sowohl beschreibenden als auch inferentiellen Statistiken ermöglicht. Auf die Gefahr hin, mich zu wiederholen, gilt alles, was oben über Intervalldaten steht, für Verhältnisskalen, und Verhältnisskalen haben eine klare Definition von Null. Gute Beispiele für Verhältnisvariablen sind Größe, Gewicht und Dauer.
Verhältnisskalen bieten eine Fülle von Möglichkeiten, wenn es um statistische Analysen geht. Diese Variablen können sinnvoll addiert, subtrahiert, multipliziert, dividiert (Verhältnisse) werden. Die zentrale Tendenz kann nach Modus, Median oder Mittelwert gemessen werden; Streuungsmaße wie Standardabweichung und Variationskoeffizient können auch aus Verhältnisskalen berechnet werden.

Zusammenfassung
Das war’s! Ich hoffe, diese Erklärung ist klar und Sie kennen die vier Arten von Datenmessskalen: Nominal, ordinal, Intervall und Verhältnis! Hol sie dir!
Wenn Sie Ihre Fähigkeiten testen möchten, probieren Sie das kurze Quiz unten aus (funktioniert nicht? Versuchen Sie es mit einem Desktop-Browser):