i statistik er der fire data måleskalaer: nominel, ordinær, interval og forhold. Dette er simpelthen måder at underkategorisere forskellige typer data på (her er en oversigt over statistiske datatyper) . Dette emne diskuteres normalt i forbindelse med akademisk undervisning og sjældnere i den “virkelige verden.”Hvis du børster op på dette koncept til en statistiktest, tak en psykologforsker ved navn Stanley Stevens for at komme med disse vilkår.
disse fire data måleskalaer (nominel, ordinær, interval og forhold) forstås bedst med eksempel, som du vil se nedenfor.
Nominel
lad os starte med den nemmeste at forstå. Nominelle skalaer bruges til mærkning af variabler uden nogen kvantitativ værdi. “Nominelle” skalaer kunne simpelthen kaldes ” etiketter.”Her er nogle eksempler nedenfor. Bemærk, at alle disse skalaer udelukker hinanden (ingen overlapning), og ingen af dem har nogen numerisk betydning. En god måde at huske alt dette på er, at “nominel” lyder meget som “navn”, og nominelle skalaer er lidt som “navne” eller etiketter.
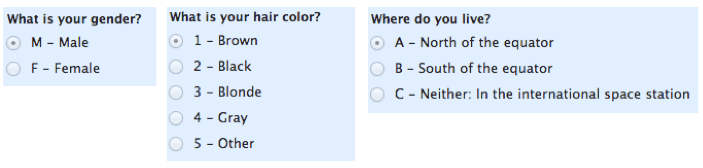
bemærk: en undertype af nominel skala med kun to kategorier (f.eks. mand/kvinde) kaldes “dikotom.”Hvis du er studerende, kan du bruge det til at imponere din lærer.
Bonusnote #2: Andre undertyper af nominelle data er” nominel med rækkefølge “(som” kold, varm, varm, meget varm”) og nominel uden ordre (som”mand/kvinde”).
Ordinal
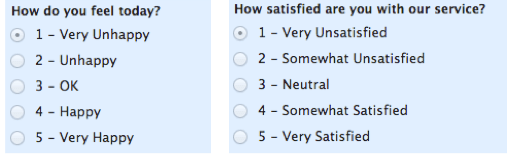
med ordinære skalaer er rækkefølgen af værdierne, hvad der er vigtigt og signifikant, men forskellene mellem hver enkelt er ikke rigtig kendt. Tag et kig på eksemplet nedenfor. I hvert tilfælde ved vi, at en #4 er bedre end en #3 eller #2, men vi ved ikke–og kan ikke kvantificere–hvor meget bedre det er. For eksempel er forskellen mellem “OK” og “ulykkelig” den samme som forskellen mellem “meget glad” og “glad?”Vi kan ikke sige.
ordinære skalaer er typisk mål for ikke-numeriske begreber som tilfredshed, lykke, ubehag osv.
“Ordinal” er let at huske, fordi det lyder som “orden”, og det er nøglen til at huske med “ordinære skalaer”–det er den rækkefølge, der betyder noget, men det er alt, hvad du virkelig får fra disse.
avanceret note: den bedste måde at bestemme central tendens på et sæt ordinære data er at bruge tilstanden eller medianen; en purist vil fortælle dig, at gennemsnittet ikke kan defineres ud fra et ordinært sæt.
Interval
Intervalskalaer er numeriske skalaer, hvor vi kender både rækkefølgen og de nøjagtige forskelle mellem værdierne. Det klassiske eksempel på en intervalskala er Celsius-temperatur, fordi forskellen mellem hver værdi er den samme. For eksempel er forskellen mellem 60 og 50 grader en målbar 10 grader, ligesom forskellen mellem 80 og 70 grader.
Intervalskalaer er gode, fordi området for statistisk analyse på disse datasæt åbnes. For eksempel kan central tendens måles efter tilstand, median eller gennemsnit; standardafvigelse kan også beregnes.
ligesom de andre kan du huske nøglepunkterne i en “intervalskala” temmelig let. “Interval” i sig selv betyder “mellemrum imellem”, hvilket er det vigtige at huske–intervalskalaer fortæller os ikke kun om ordre, men også om værdien mellem hvert element.
her er problemet med intervalskalaer: de har ikke et “sandt nul.”For eksempel er der ikke noget som “ingen temperatur”, i det mindste ikke med celsius. I tilfælde af intervalskalaer betyder nul ikke fraværet af værdi, men er faktisk et andet tal, der bruges på skalaen, som 0 grader celsius. Negative tal har også betydning. Uden et sandt nul er det umuligt at beregne forhold. Med intervaldata kan vi tilføje og trække fra, men kan ikke multiplicere eller opdele.
forvirret? Ok, overvej dette: 10 grader C + 10 grader C = 20 grader C. intet problem der. 20 grader C er dog ikke dobbelt så varmt som 10 grader C, fordi der ikke er noget som “ingen temperatur”, når det kommer til Celsius-skalaen. Når det konverteres til Fahrenheit, er det klart: 10c=50F og 20c=68F, hvilket klart ikke er dobbelt så varmt. Jeg håber, det giver mening. Bundlinie, intervalskalaer er gode, men vi kan ikke beregne forhold, hvilket bringer os til vores sidste måleskala…

Ratio
Ratio skalaer er den ultimative nirvana når det kommer til data måling skalaer, fordi de fortæller os om rækkefølgen, de fortæller os den nøjagtige værdi mellem enheder, og de har også et absolut nul–som giver mulighed for en bred vifte af både beskrivende og inferentielle statistikker, der skal anvendes. Med risiko for at gentage mig selv, alt ovenfor om interval data gælder for forholdet skalaer, plus forholdet skalaer har en klar definition af nul. Gode eksempler på forholdet variabler omfatter højde, vægt og varighed.
Ratio skalaer giver et væld af muligheder, når det kommer til statistisk analyse. Disse variabler kan meningsfuldt tilføjes, subtraheres, multipliceres, divideres (forhold). Central tendens kan måles efter tilstand, median eller middelværdi; mål for spredning, såsom standardafvigelse og variationskoefficient kan også beregnes ud fra forholdsskalaer.

sammendrag
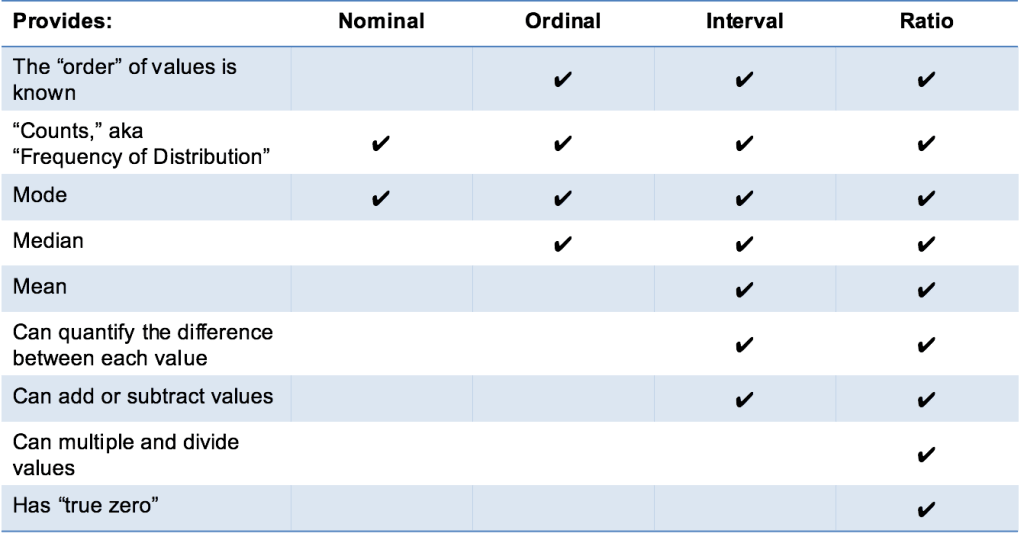
det er det! Jeg håber, at denne forklaring er klar, og at du ved, forstår de fire typer datamålingsskalaer: nominel, ordinær, interval og forhold! Hent dem!
hvis du vil teste dine færdigheder, skal du give den korte test under en gå (fungerer ikke ? Prøv på en desktop-bro. ser):