standardfejlen for middelværdien eller simpelthen standardfejl angiver, hvor forskellig befolkningsgennemsnittet sandsynligvis vil være fra et eksempelgennemsnit. Det fortæller dig, hvor meget prøven betyder, ville variere, hvis du skulle gentage en undersøgelse ved hjælp af nye prøver inden for en enkelt population.
standardfejlen for middelværdien (SE eller SEM) er den mest almindeligt rapporterede type standardfejl. Men du kan også finde standardfejlen for andre statistikker, som medianer eller proportioner. Standardfejlen er et almindeligt mål for prøveudtagningsfejl—forskellen mellem en populationsparameter og en stikprøvestatistik.
hvorfor standardfejl betyder noget
i statistikker bruges Data fra prøver til at forstå større populationer. Standardfejl betyder noget, fordi det hjælper dig med at estimere, hvor godt dine eksempeldata repræsenterer hele befolkningen.
med sandsynlighedsprøvetagning, hvor elementer i en prøve er tilfældigt valgt, kan du indsamle data, der sandsynligvis vil være repræsentative for befolkningen. Selv med sandsynlighedsprøver forbliver der dog en vis prøveudtagningsfejl. Det skyldes, at en prøve aldrig passer perfekt til den befolkning, den kommer fra med hensyn til foranstaltninger som midler og standardafvigelser.
ved at beregne standardfejl kan du estimere, hvor repræsentativ din prøve er for din befolkning og drage gyldige konklusioner.
en høj standardfejl viser, at prøvemidler er bredt spredt omkring populationsgennemsnittet—din prøve repræsenterer muligvis ikke din befolkning tæt. En lav standardfejl viser, at prøvemidler er tæt fordelt omkring befolkningens gennemsnit—din prøve er repræsentativ for din befolkning.
du kan reducere standardfejl ved at øge stikprøvestørrelsen. Ved hjælp af en stor, tilfældig prøve er den bedste måde at minimere prøveudtagning bias.
standardfejl vs standardafvigelse
standardfejl og standardafvigelse er begge mål for variabilitet:
- standardafvigelsen beskriver variabilitet inden for en enkelt prøve.
- standardfejlen estimerer variabiliteten på tværs af flere prøver af en population.


standardafvigelsen er en beskrivende statistik, der kan beregnes ud fra prøvedata. I modsætning hertil er standardfejlen en inferentiel statistik, der kun kan estimeres (medmindre den reelle populationsparameter er kendt).
standardafvigelsen for matematikresultaterne er 180. Dette tal afspejler i gennemsnit, hvor meget hver score adskiller sig fra den gennemsnitlige prøve på 550.
standardfejlen for matematiske scoringer fortæller dig på den anden side, hvor meget den gennemsnitlige prøve score på 550 adskiller sig fra andre prøve gennemsnitlige score, i prøver af samme størrelse, i populationen af alle testtagere i regionen.
standardfejlformel
standardfejlen for gennemsnittet beregnes ved hjælp af standardafvigelsen og stikprøvestørrelsen.
fra formlen vil du se, at prøvestørrelsen er omvendt proportional med standardfejlen. Dette betyder, at jo større prøven er, desto mindre er standardfejlen, fordi stikprøvestatistikken vil være tættere på at nærme sig populationsparameteren.
forskellige formler anvendes afhængigt af om populationsstandardafvigelsen er kendt. Disse formler arbejder for prøver med mere end 20 elementer (n > 20).
når populationsparametre er kendt
når populationsstandardafvigelsen er kendt, kan du bruge den i nedenstående formel til at beregne standardfejl præcist.
| formel | forklaring |
|---|---|
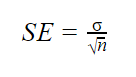 |
|
når populationsparametre er ukendte
når populationsstandardafvigelsen er ukendt, kan du bruge nedenstående formel til kun at estimere standardfejl. Denne formel tager prøvestandardafvigelsen som et punktestimat for populationsstandardafvigelsen.
| formel | forklaring |
|---|---|
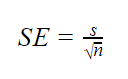 |
|
find først kvadratroden af din stikprøvestørrelse (n).
| formel | beregning |
|---|---|
| √n | n = 200
ren n = √200 = 14.1 |
divider derefter prøvestandardafvigelsen med det nummer, du fandt i trin et.
| formel | beregning |
|---|---|
| SE = s ren n | s = 180
ren n = 14,1 s Ren n = 180 ÷ 14.1 = 12.8 |
standardfejlen for math SAT-scoringer er 12,8.
hvordan skal du rapportere standardfejlen?
du kan rapportere standardfejlen sammen med gennemsnittet eller i et konfidensinterval for at kommunikere usikkerheden omkring gennemsnittet.
den bedste måde at rapportere standardfejlen på er i et konfidensinterval, fordi læsere ikke behøver at lave yderligere matematik for at komme med et meningsfuldt interval.
et konfidensinterval er et interval af værdier, hvor en ukendt populationsparameter forventes at ligge det meste af tiden, hvis du skulle gentage din undersøgelse med nye tilfældige prøver.
med et 95% konfidensniveau forventes 95% af alle stikprøvemidler at ligge inden for et konfidensinterval på 1,96 standardfejl i stikprøvegennemsnittet.
baseret på tilfældig prøveudtagning estimeres den sande populationsparameter også at ligge inden for dette interval med 95% tillid.
for en normalt distribueret karakteristik, som SAT-scoringer, falder 95% af alle prøveorganer inden for omtrent 4 standardfejl i prøvegennemsnittet.
| konfidensinterval formel | |
|---|---|
|
CI = SE = standardfejl = 12.8 |
|
| nedre grænse | øvre grænse |
|
H − (1.96 Karin SE) 550 − (1.96 × 12.8) = 525 |
k + (1,96 kr. SE) 550 + (1.96 × 12.8) = 575 |
med stikprøveudtagning fortæller en 95% CI dig, at der er en 0,95 Sandsynlighed for, at befolkningen betyder matematik SAT score er mellem 525 og 575.
andre standardfejl
bortset fra standardfejlen for gennemsnittet (og anden statistik) er der to andre standardfejl, du måske støder på: standardfejlen for estimatet og standardfejlen for måling.
estimatets standardfejl er relateret til regressionsanalyse. Dette afspejler variabiliteten omkring den estimerede regressionslinje og nøjagtigheden af regressionsmodellen. Ved hjælp af estimatets standardfejl kan du konstruere et konfidensinterval for den sande regressionskoefficient.
standardmålingsfejlen handler om pålideligheden af et mål. Det angiver, hvor variabel målefejlen for en test er, og det rapporteres ofte i standardiseret test. Standardmålingsfejlen kan bruges til at oprette et konfidensinterval for den sande score for et element eller et individ.
ofte stillede spørgsmål om standardfejl
standardfejlen for middelværdien eller simpelthen standardfejl angiver, hvor forskellig populationsgennemsnittet sandsynligvis vil være fra et eksempelgennemsnit. Det fortæller dig, hvor meget prøven betyder, ville variere, hvis du skulle gentage en undersøgelse ved hjælp af nye prøver inden for en enkelt population.
standardfejl og standardafvigelse er begge målinger af variabilitet. Standardafvigelsen afspejler variabilitet inden for en prøve, mens standardfejlen estimerer variabiliteten på tværs af prøver af en population.
ved hjælp af beskrivende og inferentiel statistik kan du lave to typer estimater om befolkningen: punktestimater og intervalestimater.
- et punktestimat er et enkelt værdiestimat for en parameter. For eksempel er et eksempelgennemsnit et punktestimat af et populationsgennemsnit.
- et intervalestimat giver dig en række værdier, hvor parameteren forventes at ligge. Et konfidensinterval er den mest almindelige type intervalestimat.
begge typer estimater er vigtige for at samle en klar ide om, hvor en parameter sandsynligvis vil ligge.
