hvordan beregnes P-værdien?

Indholdsfortegnelse

1. 1. Hvad Er P-Værdien?
   2. Hvorfor Har Vi Brug For P-Værdien?
   3. Hvor Bruger Vi P-Værdien I Det Virkelige Liv?
      • markedsføring
      • Sandsynlighed
   4. Hvordan beregner jeg p-værdien?
   5. afsluttende ord

Hvad er p-værdien?

P-værdi er et statistisk udtryk, der hjælper dig med at bestemme, om den hypotese, du bruger, er sand, sandsynligheden for prøveudtagningsvariationen. Det fortæller os simpelthen, hvad der er oddsene for at få disse resultater, hvis vores nulhypotese er sand.

• en nulhypotese er en hypotese, der hævder, at de resultater, vi får, er forårsaget af rent held.
• en alternativ hypotese hævder, at de resultater, vi får, ikke er heldige, men der er eksterne elementer, der påvirker vores resultater.

det er et meget vigtigt og almindeligt anvendt statistisk udtryk og kan let beregnes i dataanalyseprogrammer som f.eks. I denne artikel lærer du, hvordan vi bruger det, hvor bruger vi det, og hvordan kan vi beregne det i udmærke sig på forskellige måder.

lad os begynde!

Hvorfor Har Vi Brug For P-Værdien?

mens du laver forskning med store populationer, skal du beregne statistikken for hver enkelt person. Men selv i et sådant tilfælde kan du ikke være sikker på, om der sker noget på grund af tilfældighed eller bare held, da det er umuligt at observere alt. Det er her statistikkerne kommer ind.

statistiske beregninger kan ikke give dig en absolut sandhed, men de vil hjælpe dig med at få en god ide om dine undersøgelser.

P-værdi giver os mulighed for at teste hypotesen om vores emne. Vi kan sammenligne de matematiske resultater med disse hypoteser og genoverveje vores vej uden at bruge meget tid på forskning.

Hvor Bruger Vi P-Værdien I Det Virkelige Liv?

vi bruger sandsynlighedsværdien, hvor vi forsøger at teste en hypotese. Det kan være om forskning eller en simpel indsats, vi lavede med vores ven.

det er lettere at forstå det med eksempler.

Marketing:

lad os sige, at du arbejder inden for marketingområdet, og dit seneste projekt er på kornannoncering.

du har produceret en video til sociale medier, og du har fået informationen til snarere brugere sprunget over den eller set den i lang tid.

som et eksempel er den almindelige visningstid for videoen 20 sekunder. Gennemsnittet er 20 sekunder. Og du tog beslutningen om at redigere videoen med en del mere glad musik.

hvordan vil du nu genkende, om det fungerede? På dette tidspunkt bruger vi signifikansstatistikker.

fremstil først en nulhypotese:

en nulhypotese hævder, at der ikke er nogen sammenhæng mellem det, du investerer, og de resultater, du får. Det påvirker ikke resultaterne.

i dette eksempel vil nulhypotesen være dette: “der er ikke noget forhold mellem de ændringer, du anvender på uret.”

derefter den alternative hypotese:

den alternative hypotese antyder, at faktisk ændring af musikken fungerede, og nu ser folk reklamen i mere end 20 sekunder. Matematisk siger den alternative hypotese:

” middelværdien er større end 20 sekunder nu.”

Beregn signifikansniveauet:

nu skal vi indstille en grænsetærskel for at beregne, om vi har succes eller ej. Dette kaldes et signifikansniveau kaldes desuden alfa-værdien. Det kan være en hvilken som helst procentdel, du ønsker, det er helt op til dig.

men under dette eksempel vil det være 0,05.

nu for at beregne med sikkerhed skal vi altid have alle data om uret. Men hvad angår din tid og kilder, skal du tage en prøve fra befolkningen:

1. du tog en prøve på 100 personer.
2. disse 100 personer har 25 sekunders tid til reklamen.
3. det betyder, at prøven gennemsnit er 25.

dette er en meget enkel version af beregningen. Men standardafvigelsen for prøven beregnes normalt i denne skala, hvis du ikke kender standardafvigelsen for hele befolkningen.

du kan bruge de værdier, du har beregnet for prøven, da de er tæt på befolkningsværdierne. Stikprøvegennemsnittet er tæt på populationsgennemsnittet.

Beregn P-værdien:

p-værdien viser os, om vi kan afvise nulhypotesen eller ej. Sandsynligheden for, at prøvegennemsnittet er større end eller lig med 25 minutter givet nulhypotesen er sand.

der er to situationer, der kan ske.

1. hvis p-værdien er mindre end alfa, kan du afvise nulhypotesen. Du har statistisk bevis for, at den alternative hypotese er sand.
2. men hvis p-værdien er større eller lig med alfa, kan du ikke afvise nulhypotesen. Det betyder ikke, at nulhypotesen helt sikkert er sand, men det kan heller ikke undgås.

Sandsynlighed

lad os arbejde på et andet eksempel.

din ven og du lavede kaste mønt i luften: hvis det er haler, mister du 5 dollars, og hvis det kommer hoveder, får du 5 dollars.

• din ven vender mønten en gang: den kommer som haler. Det er okay, der er en 50% chance for, at det kommer som haler. Nu antager du sandsynligheden er 0,5, fordi du mener, det er en retfærdig mønt. Dette er din nulhypotese.

• sekund: det er haler. Du mistede yderligere 5 dollars, men det er okay, fordi der stadig er en god chance for to haler i træk. P-værdien er 0,25, og det er stadig et rimeligt forhold.
• tredje: det er haler igen. Chancen for haler tre gange i træk er 0,12. Det er ikke lavt, så der er ikke nok bevis for, at nulhypotesen ikke er korrekt. Men du begynder at tro, at din alternative hypotese kunne være korrekt.
• fjerde: det bliver som haler igen, du vil se, hvordan chancerne bliver virkelig lave. Det kan være en mirakuløs tilfældighed, men der er stadig en 0,6 chance, og der er stadig ikke nok beviser til at understøtte den alternative hypotese, der siger, at mønten er vanskelig. Og du venter på den femte flip.
• femte: det er haler. Chancen for en mønt viser sig som haler fem gange i træk er 0,3 hvilket er meget lav. Dette er det punkt, du kan afvise nulhypotesen, for der er ikke nok bevis til at understøtte det længere.

du beder din ven om at se mønten, og når du holder den, indser du, at den har to haler side, og det er en vanskelig mønt.

Hvad fik os til at miste troen på vores nulhypotese?

i et fair spil med at vende mønter er chancen for at få hoveder eller haler 50%. Dette er en situation, hvor vi mener, at mønten er retfærdig, men da p-værdien falder, svækkes vores tillid til den hypotese også.

der er ringe chance for at have tilfældige haler, når p-værdien falder under 0,05. Så når du anvender dette statistiske udtryk på spørgsmål som kræftforskning eller virkninger af klimaændringer, får det større betydning.

 Bemærk: Der er ingen specifik grund til, at vi bruger 0,05 p-værdi til standardberegning. Skaberen af formlen besluttede, at det var et godt tal til beregning, og standardberegningerne holder fast ved det. 0,05 betyder 5% i 100 individer populationer, der falder ind i den normale kurve. Dette er en af grundene til, at det ofte bruges. Hvis du vil ændre det under beregning af det selv, kan du.

hvordan beregnes P-værdien?

der er mere end en måde at beregne p-værdien på. Du kan skrive ned formler, eller du kan bruge analyse ToolPak. Denne artikel indeholder, hvordan man gør det begge veje.

brug af klassiske formler:

lad os starte med den klassiske formel. Der er to måder at gøre denne tdist formel og T-test formel.

1.1) Tdist formel

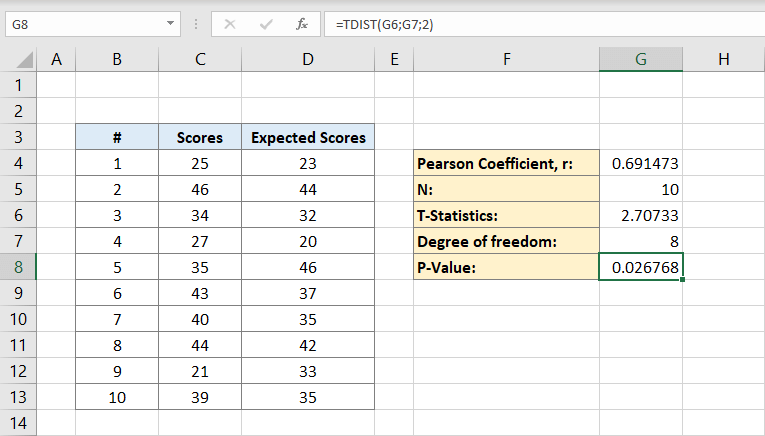
først og fremmest skal du bruge et datasæt til at beregne en p-værdi.

• lad os sige, at du er lærer, og du vil sammenligne, hvad dine elever scorede i din sidste eksamen, og hvad du forventede, at deres score skulle være baseret på deres tidligere eksamener.
• du har resultaterne 25, 46, 34, 27, 35, 43, 40, 44, 21 og 39 til din seneste eksamen.
• nu til beregning har du brug for en anden hale, dette er den score, du forventede baseret på tidligere tests: 23, 44, 32, 20, 46, 37, 35, 42, 33, og 35

for at bruge p-værdiformlen skal du nu beregne et par ting på forhånd:

Pearson-koefficient (r): Det er et statistisk udtryk, der måler den lineære sammenhæng mellem to data. Du behøver ikke at kende det matematiske aspekt af det for at beregne p-værdien. Du vil se den enkle formel for det i de næste afsnit.

befolkning (n): n er det samlede antal personer i dit datasæt.

t statistik: det er forholdet mellem afvigelsen af data estimeret værdi fra dens antagne værdi til dens standardfejl.

grad af frihed: det er antallet af individer i datasættet minus to.

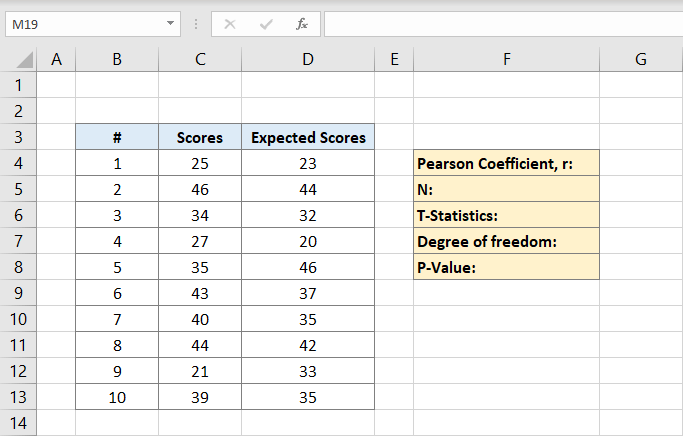
nu vil Pearson-koefficienten blive skrevet på F4 i dette eksempel. Når du har klikket på det, skriver du formlen:

C kolonner er for scorerne og D kolonner er for de forventede scoringer. Pearson-koefficienten er 0,691473 i dette eksempel.

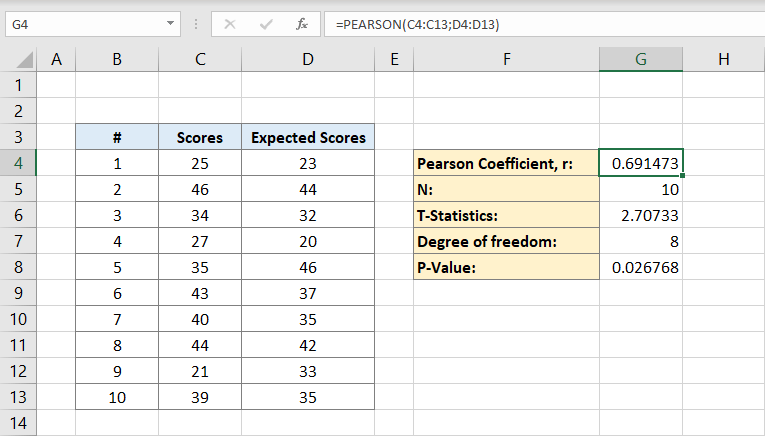
dernæst skriver du antallet af personer i datasættet. Hvis du helt sikkert ved, hvor mange personer du har, kan du skrive det manuelt, men hvis du ikke gør det, kan du bruge formlen:

hvorfor indeholder formlen kun en C-kolonne?

det er fordi vi kun har brug for individerne i et datasæt til at beregne, derfor vil en kolonne gøre. Cellen G5 vil nu indeholde nummeret 10 i den. Det er vores befolkning.

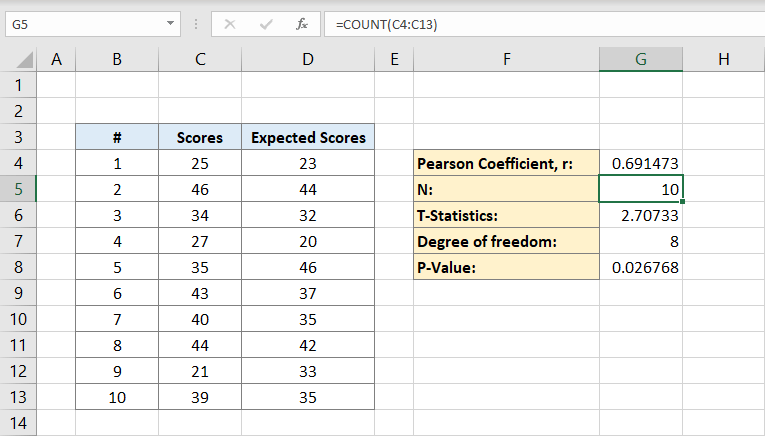
nu hvor du har både Pearson-koefficienten og befolkningen, kan du beregne t-statistikker. Den matematiske formel for T statistik er Pearson koefficient (r) gange tegn kvadratroden af befolkningen (n) minus 2 divideret med kvadratroden af 1 minus Pearson koefficient kvadreret:

cellen G6 vil indeholde resultatet 2,70733. Dette er vores T statistik.

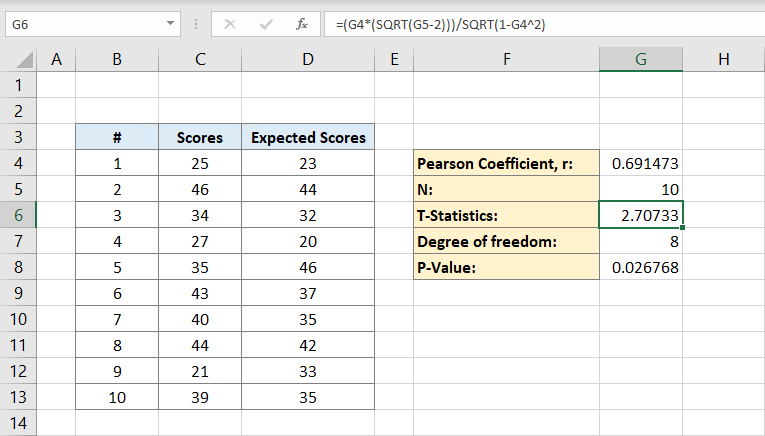
derefter beregner du graden af frihed. Du skriver:

til cellen G7. Dette er graden af frihed. Det bliver klokken 8.

nu har du alt hvad du behøver for at beregne P-værdien. Cellen G8 vil indeholde formlen for den. Det vil sige:

eller

resultatet bliver 0,026768. Dette er p-værdien for datasættet.

1.2. T-Test formel

den anden måde at bestemme p-værdien med udmærker formler er ved hjælp af T-test formel. Det ligner lidt det foregående eksempel, men kortere.

• lad os sige, at datasættet er det samme, du har resultaterne 25, 46, 34, 27, 35,43, 40, 44, 21, 39 til din seneste eksamen.
• forventede resultater er 23, 44, 32, 20, 46, 37, 35, 42, 33, 35.
• du skal tilføje en tredje kolonne for forskellen mellem hvad der var forventet og den faktiske score. I kolonnen Forskel 2, 2, 2, 7, 11, 6, 5, 2, 12, 4 vil blive skrevet fra E4 til E13.

skriv nu T-Test til cellen E8. Du skal skrive t-testformlen til den tomme celle ved siden af den. Det vil sige:

og denne formel giver dig p-værdien direkte.

Bestem P-værdien med Pak

tog Pak er en pakke, der giver dig mulighed for at beregne forskellige statistiske målinger automatisk, så det er nemt og meget praktisk. Det er også nemt at installere.

Trin 1: Gå til Indstillinger. Der er en” Add-ins ” – knap nederst i venstre hjørne, Klik på den. Et nyt vindue vises, find indstillingen” analyseværktøj Pak”, klik på det, og klik derefter på go-knappen nederst i vinduet.

Trin 2: Aktiver tilføjelsesprogrammet ved at klikke på krydssymbolet ved siden af det og efter OK-knappen i højre kolonne.

Trin 3: Hvis det lykkedes dig at aktivere det korrekt, vises en “dataanalyse” – knap i topmenuen i dit regneark til højre.

Trin 4: Klik på knappen “dataanalyse”, og vælg indstillingen “T-Test: parret to Prøve for midler”. Klik på OK efter det. Et nyt vindue vises.

Trin 5: det spørger indgangene i den første række i vinduet. Type C4: C13 til boksen “variabel 1 rækkevidde”. Du skriver D4: D13 til feltet” variabel 2 rækkevidde”. Forlad alfa-boksen med standardværdien.

Trin 6: i den anden række i vinduet kan du vælge, hvor du skal overvåge dine resultater. Det kan være et nyt regneark eller tomme celler. Hvis du vil have resultatet på en celle, skal du sørge for at låse kolonnen og rækken. Klik derefter på OK-knappen.

 Tip: Brug dollartegnet før bogstavet og nummeret til at låse kolonnen og rækken. For eksempel, hvis du vil låse A2-celle, skriver du $a$2.

Trin 7: udmærke vil beregne middelværdi, varians, observationer, Pearson korrelation, hypotetisk middelforskel, t statistik, p-værdi og meget mere.

afsluttende ord

P-værdi er let at beregne og tilpasse i mange forskellige situationer. Det hjælper dig med at få de oplysninger, du har brug for uden at bruge en masse tid eller kræfter på det. Det er endnu nemmere at beregne, når du bruger statistiske analyseprogrammer som f.eks. Lad os tjekke someka skabeloner samling og hente statistiske skabeloner til at gøre dit job lettere!

relaterede aflæsninger:

• hvordan beregnes konfidensintervallet?
• Kan Du Analysere Data?